Intro
On previous questions where I am trying to understand ODEs that have solutions that stop moving in finite time (example 1, example2), due other users answers (@md2perpe, @RollenS.D'Souza), I realized that maybe is not necessarily to start from a solution achieve rest at zero in finite time and integrate it in order to have something that stop moving at a place different from zero.
As example, let think in a 2nd order linear ODE with real-valued positive constant coefficients:
$$\begin{array}{c} y''+a y'+by+c = 0, \\ y[0]=y_0,\, y'[0]=y'_0 \end{array} \tag{Eq. 1}\label{Eq. 1}$$
I want to know if it is valid to define a solution for some finite extinction time $0<T<\infty$ where the solution $y(t)$ behaves like $y'[T]=0$ to redefine the ODE into something that stop moving there, like: $$\boxed{h(t) = y[T]-\left(y[T]-y(t)\right)\theta(T-t)}\quad \Rightarrow \quad h(0)\equiv y(0)\quad\wedge\quad h(T)\equiv y(T)\tag{Eq. 2}\label{Eq. 2}$$ which should be fulfilling the differential equation: $$\begin{array}{c} h''+ah'+bh+c-\left(bh[T]+c\right)\theta(t-T)=0,\\ h'[T]=y'[T]=0,\, h[0]=h_0=y_0,\,h'[0]=h'_0=y'_0 \end{array} \tag{Eq. 3}\label{Eq. 3}$$
where $\theta(t)$ is the Heaviside step function.
Main analysis
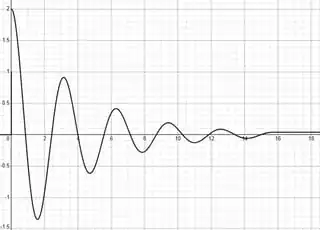
To visualize if this is working I tried the following example: $$y''+\frac12 y'+\frac{65}{16}y = 0,\quad y[0]=2,\, y'[0]=0 \tag{Eq. 4}\label{Eq. 4}$$ which leads to the solution: $$y(t) = \dfrac{e^{-\frac{t}{4}}}{4}\left(8\cos(2t)+\sin(2t)\right) \tag{Eq. 5}\label{Eq. 5}$$ This is an oscillatory solution, so analyzing its derivative $y'(t) = -\dfrac{65 e^{-\frac{t}{4}}}{16}\sin(2t)$ which have zeros associated the the local maxima at $n\pi$, and zeros associated the the local minima at $n\pi\pm\frac{\pi}{2}$, $n$ integer. For the following example I arbitrarily choose to have $T = 5\pi$, which leads to $h[T] = h[5\pi] = 2e^{-\frac{5\pi}{4}}$ so \eqref{Eq. 3} takes the form: $$\begin{array}{c} h''+\frac12 h'+\frac{65}{12} h-\frac{65}{8}e^{-\frac{5\pi}{4}}\theta(t-5\pi)=0,\\ h[0]=2,\,h'[0]=0\end{array} \tag{Eq. 6}\label{Eq. 6}$$ When I tried the differential equation in Wolfram-Alpha it do delivers the answer corresponding to \eqref{Eq. 2}:
$$h(t) = 2e^{-\frac{5\pi}{4}}-\left(2e^{-\frac{5\pi}{4}}-\dfrac{e^{-\frac{t}{4}}}{4}\left(8\cos(2t)+\sin(2t)\right)\right)\theta(5\pi-t)\tag{Eq. 7}\label{Eq. 7}$$ which can be seen is working as intended in Desmos.
As you can see in the image, the solution to \eqref{Eq. 6} do behave as the oscillating decaying solution of \eqref{Eq. 5} but it stops moving at time $t=5\pi\approx 15.7$.
Question
How these kind of ODEs named? I want to know if these are valid ODEs, if their solutions are unique, why they work, where they have been applied, among others: Are they Filippov's?
PS: I already realized that the same analysis don't work for first order linear ODEs with real-valued constant coefficients since their solutions are non-oscillatory exponentials, which don't have a finite time were $y'[T]=0$ could happen.
How I get \eqref{Eq. 3} (just in case is needed) - Not mandatory reading
First I started by differentiating \eqref{Eq. 2}: $$\begin{array}{r c l} h'(t) & = & \underbrace{\require{cancel}\cancel{y[T]}}_{\text{constant term}}-\underbrace{\left(y[T]-y(t)\right)\delta(T-t)(-1)}_{\text{only nonzero when }t=T}-\left(\underbrace{\require{cancel}\cancel{y[T]}}_{\text{constant term}}-y'(t)\right)\theta(T-t) \\ & = & \require{cancel}\cancel{\underbrace{\left(y[T]-y[T]\right)}_{=\,0\,\text{at time }t=T}\delta(0)}+y'(t)\theta(T-t)\\ \Rightarrow h'(t) & = & y'(t)\theta(T-t) \quad \Rightarrow\quad h'(0)\equiv y'(0) \tag{Eq. 8}\label{Eq. 8} \end{array}$$ where $\delta(x)$ it is the Dirac Delta Function. Then, by differentiating again \eqref{Eq. 8}: $$\begin{array}{r c l} h''(t) & = & y''(t)\theta(T-t)+\underbrace{y'(t)\delta(T-t)(-1)}_{\text{only nonzero when }t=T}\\ & = & y''(t)\theta(T-t)-\require{cancel}\cancel{\underbrace{y'[T]}_{=\,0\,\text{by assumption}}\delta(0)}\\ \Rightarrow h''(t) & = & y''(t)\theta(T-t) \tag{Eq. 9}\label{Eq. 9} \end{array}$$ where $y'[T]=0$ by the assumption we picked $T$ such $\exists\, T\, /\, y'[T]=0$.
With these, I think of a 2nd order ODE in general form: $$y''(t) = F\left(y(t),y'(t)\right)\tag{Eq. 10}\label{Eq. 10}$$ and multiplied it by $\theta(T-t)$ such I make appear the term $h''(t)$: $$\underbrace{y''(t)\theta(T-t)}_{\displaystyle{h''(t)}} = F\left(y(t),y'(t)\right)\theta(T-t)\tag{Eq. 11}\label{Eq. 11}$$ then I isolate $y(t)$ in terms of $h(t)$ in \eqref{Eq. 2} and also isolated $y'(t)$ in terms of $h'(t)$ in \eqref{Eq. 2} and I replaced on \eqref{Eq. 11} finding a general formula in terms of the change of variable: $$h''(t) = F\left(h[T]+\frac{(h(t)-h[T])}{\theta(T-t)},\frac{h'(t)}{\theta(T-t)}\right)\theta(T-t)\tag{Eq. 12}\label{Eq. 12}$$ and ignoring that $1/\theta(T-t)$ is undefined for $t\geq T$ (which is not an issue since I cared only for the solution before a singular point when the solution stops moving), I applied \eqref{Eq. 12} to the equation of \eqref{Eq. 1} and it becomes \eqref{Eq. 3}, showing exactly the Non-Lipschitz term I need to subtract to make a differential equation with a solution that stops moving: $$h''+ah'+bh+c-\underbrace{\left(bh[T]+c\right)\theta(t-T)}_{\text{extra Non-Lipschitz term}}=0 \tag{Eq. 13}\label{Eq. 13}$$
and I also tested it and only works if the time $T$ is choose such $h'[T]=0$: if you pick just some random $0<\hat{T}$ such $h'[\hat{T}]\neq 0$ you get some weird $h(t)$ that keeps moving.
Also, coincidentally I tested it on a differential equation I knew beforehand it stops moving at zero (details here): $y''(t) = -\text{sgn}(g'(t))$ and it just become after applying \eqref{Eq. 12} $h''(t) = -\text{sgn}(h'(t))$ as it should, but I believe is just because $y''(t)$ was independent of $y(t)$ in this case (later I will try it with something that includes $y(t)$ to see if I could learn something from it).
Last comment: notice in \eqref{Eq. 2} that since $\theta(t-T)+\theta(T-t)=1$ we have the equivalence: $$h(t) = y[T]-\left(y[T]-y(t)\right)\theta(T-t)\equiv y(t)\theta(T-t) +y[T]\theta(t-T) \tag{Eq. 14}\label{Eq. 14}$$