Assume you want to solve a system of non-linear equations $$f_1(x,y)=0\\ f_2(x,y)=0$$ $x,y \in [0,1]$ and $f_i : [0,1]^2 \rightarrow \mathbb{R}$, but derivatives and finite differences are not available or too costly.
The literature for this case is very sparse. I found a method called Characteristic Bisection which is a multidimensional generalization of the Bisection algorithm.
To improve on that I had the idea of a simple generalization of the Secant method:
- sample initial set of points $(x_i,y_i)$ in the domain and calculate $f_1,f_2$ for these
- Delaunay-triangulate the domain using these points
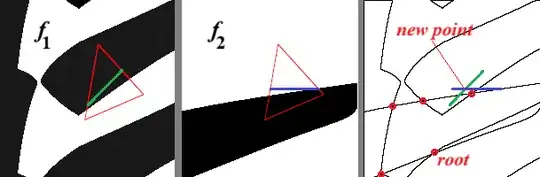
- for every triangle $(v_1,v_2,v_3)$ such that: $f_1$ changes sign at the vertices & $f_2$ changes sign at the vertices do
- intersect the plane through the points $(v_i,f_1(v_i))$ with the plane $z=0$ to get line $l_1$
- intersect the plane through the points $(v_i,f_2(v_i))$ with the plane $z=0$ to get line $l_2$
- intersect the lines $l_1$ and $l_2$ to get a point $(x',y')$
- if $(x',y')$ is in the triangle add it to the set of points
- iterations++ and go to step 2 or stop if number of iterations reached
Here is an example to get the idea. Values of $\text{sign}(f_i)$ in black/white and the resulting line (left, mid) and their intersection (right).
What's the name of that algorithm (if it has been investigated before) or if not, would it actually work? Are there pitfalls or ways to improve? Thanks in advance!
Addendum: If all triangles in an area are too large it is possible to miss a root. Flipping edges in the triangulation might reduce that.