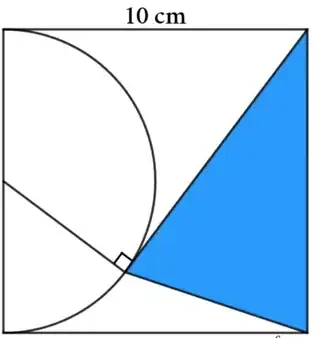
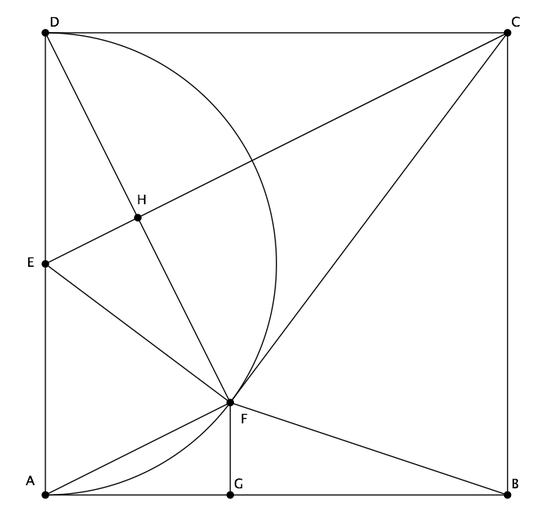
In the following square, a semi-circle and a tangent line to it is drawn. What is the area of the shaded region?
I solved it as follows:
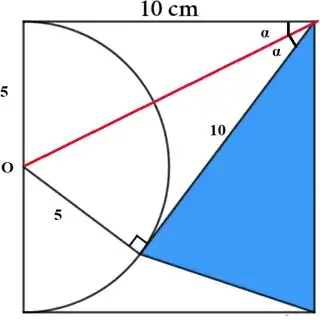
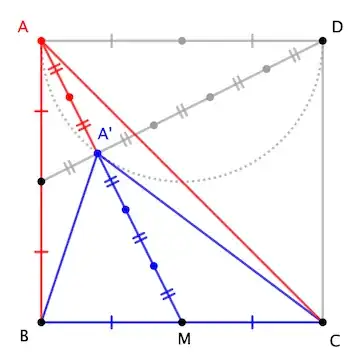
We have $\tan\alpha=1/2$, and area of the shaded triangle is equal to
$$\dfrac12\times10\times10\times\sin(90^{\circ}-2\alpha)=50\sin(90^{\circ}-2\alpha)$$
From $\tan\alpha=1/2$, we have $\tan(2\alpha)=\dfrac{1}{1-(1/2)^2}$ and $\tan(90^{\circ}-2\alpha)=1-(1/2)^2=3/4$.
Now, drawing the $3-4-5$ triangle, we can see that $\sin(90^{\circ}-2\alpha)=3/5$ and the area of the blue triangle is $30 \text{cm}^2$.
I am looking for other methods to solve this problem without trigonometry.
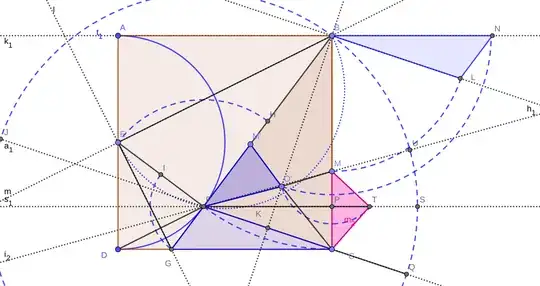
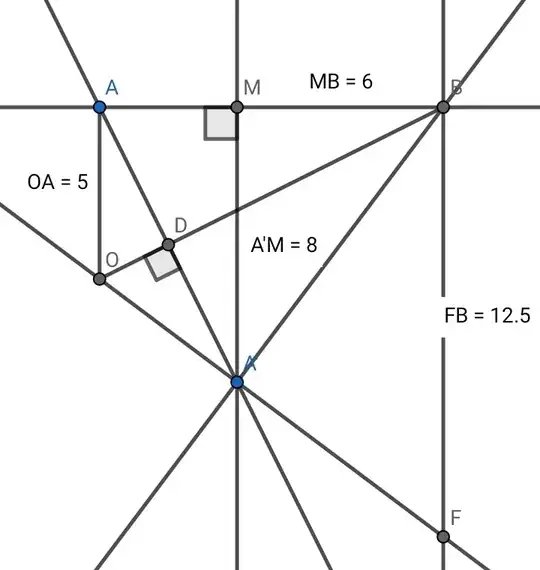
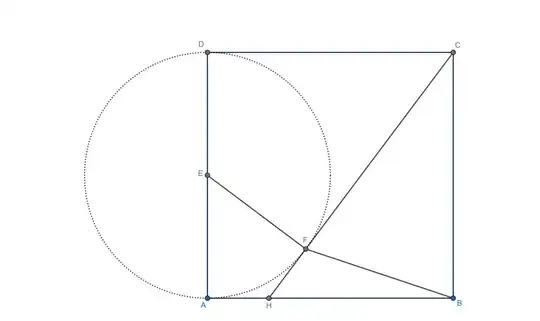
Quite separately, respectthecone's Post seems to depend on a point 'y…' which to me, anyway, isn't visible in the diagram…
Will anyone say what I missed, in either case?
– Robbie Goodwin May 28 '25 at 21:25