0

Given a cubic Bézier curve with control points P0, P1, P2, P3, is there a way to determine whether it approximates a circular arc using only those four points — without evaluating the curve at intermediate t values?

I understand that any such test would need to allow for a tolerance parameter, since a cubic Bézier curve cannot exactly represent a circular arc by definition.

One idea I have is to evaluate the midpoint of the Bézier, fit a circle through P0, that midpoint, and P3, then compare the tangents implied by the control polygon to those of the fitted circle at the endpoints. But I’m wondering if there’s a way to do something like this without sampling at all — using only the control points directly.

Is there a known geometric or algebraic method for testing approximate circularity of a cubic Bézier from its control polygon alone?

J. W. Tanner
  • 63,683
  • 4
  • 43
  • 88
jwezorek
  • 269
  • The curve is contained in the convex quadrangle of the control points, you can get a first simple error bound. This can be improved significantly by splitting the curve at its midpoint (at the cost of 12 additions and 6 divisions by 2) which gives you two much smaller quadrangles (at least if the curve is not a ridiculously bad approximation of the arc) – Hagen von Eitzen May 16 '25 at 22:02
  • what simple error bound? – jwezorek May 16 '25 at 22:51
  • Do you assume a symmetry of points $P_0 \leftrightarrow P_3$, $P_1 \leftrightarrow P_2$ with respect to a common line ? – Jean Marie May 17 '25 at 12:53
  • There are several ways to evaluate how well a cubic Bézier curve fits a circular arc. Eg, radial drift, or how well the area of the Bézier sector approximates the circular sector area. Also, you can get closer approximations if $P_0$ & $P_3$ don't lie exactly on the circular arc. See https://math.stackexchange.com/q/873224/207316 & https://spencermortensen.com/articles/bezier-circle/ – PM 2Ring May 18 '25 at 01:22

1 Answers1

3

Let us consider a prototypal case (see figure)

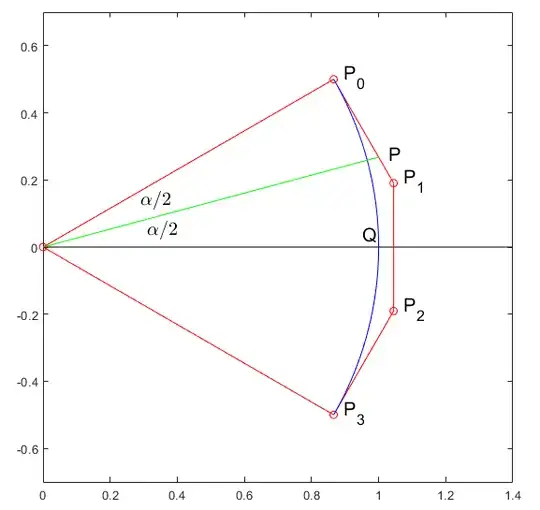
enter image description here

Fig. 1.

where we assume :

  1. that there exist a line of symmetry making $P_2$ and $P_3$ the images of $P_1$ and $P_0$ resp.

  2. that, moreover, up to a rotation, a translation and a homothety, point $P_0$ can be chosen WLOG with coordinates

$$(a,b)=(\cos \alpha,\sin \alpha) \ \ \text{ where} \ \ 0<\alpha<\pi/2.$$

In this way, the issue is reduced to understand how $P_1$ must be chosen knowing $\alpha$.

We are going to show that the ideal option is by choosing $P_1$ on the orthogonal line $(\ell)$ to $OP_0$ issued from $P_0$ such that $\vec{P_0P_1}=\tfrac43 \vec{P_0P}$ where $P$ is the point on line $(\ell)$ such that $\angle POP_0=\tfrac12 \alpha$.

Otherwise said :

$$\underbrace{\|\vec{P_0P_1}\|}_k=\tfrac43 \tan(\tfrac12 \alpha)\tag{1}$$

Here is why.

Let us write the expression of the cubic Bézier under the form :

$$M=s^3P_0+3s^2tP_1+3st^2\overline{P_1}+t^3\overline{P_0} \ \ \text{where} \ \ s:=1-t$$

Let us expand it :

$$M=s^3(a+ib)+3s^2t(a+ib-ki(a+ib))+3st^2(a-ib+ki(a-ib))+t^3(a-ib)\tag{2}$$

Now consider the case where $M$ is the midpoint $Q$ of the arc (case $s=t=\tfrac12$).

One can consider that the circularity will be optimal by constraining $Q$ to be at abscissa $\color{red}{1}$ on the $x$ axis. In this way we will have $OQ=OP_0=OP_3=1$.

Taking $s=t=\tfrac12$ in (2) gives :

$$\tfrac18((a+ib)+3(a+kb)+3(a+kb)+(a-ib))=\color{red}{1}$$

Setting $a=\cos \alpha, \ b=\sin \alpha$, we get

$$8 \cos \alpha + 6 k \sin \alpha = 8$$

$$k=\frac{4(1- \cos \alpha)}{3 \sin \alpha}$$

$$k=\frac{4 \times 2 \sin^2(\alpha/2)}{3 \times 2 \sin (\alpha/2) \cos(\alpha/2)}$$

Simplifying, one gets the value of $k$ given in (1).

It is interesting to have an idea of the local (and global) discrepancy of the Bezier arc wrt to a circular arc. it is represented on Fig. 2. In the case of angle $\alpha=\tfrac{\pi}{6}$ taken in Fig. 1, one sees that the relative maximal discrepancy is good ($\approx 2.5 \times 10^{-5}$).

Remark : I just had a look at this reference given by @PM 2Ring giving exactly the same expression (2), though with a different approach.

Even better approximations could be achieved, by moving very slightly $P_0, Q, P_3$ as explained in this reference. But my personal opinion is that it is not useful because it is so easy to have exact circular arcs by turning to rational Bézier curves !

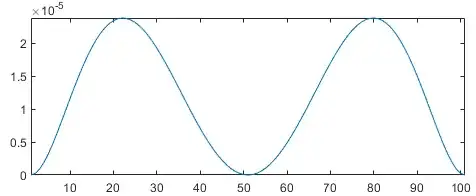
enter image description here

Fig. 2.

Appendix : Matlab program for the generation of Fig. 1 and Fig. 2 :

 clear all;close all;                                               
 an=pi/6;k=(4/3)*tan(an/2);P0=exp(i*an);P3=conj(P0);                                                 
 P1=(1-k*i)*P0;P2=conj(P1);                                               
 PP=[P0,P1,P2,P3];                                               
 p=0.7;plot([0,2*p],[0,0],'-k');hold on;                                             
 plot([0,PP,0],'-or');axis equal;axis([0,2*p,-p,p])                                               
 t=0:0.01:1;s=1-t;                                               
 f=PP*[s.^3;3*s.^2.*t;3*s.*t.^2;t.^3];plot(f,'b'); % cubic Bézier                                               
 P=1+i*tan(an/2);                                              
 plot([0,P],'-g');                                               
 Q=0.92+0.03i;L=[PP,P,Q];                                               
 set(gcf,'defaulttextfontsize',15)                                               
 text(real(L)+0.03,imag(L)+0.01,{'P_0','P_1','P_2','P_3','P','Q'});                                                
 text([0.29,0.31],[0.14,0.05],{'$\alpha/2$','$\alpha/2$'},'Interpreter','latex');
 figure                              
 plot(abs(f)-1)
Jean Marie
  • 88,997
  • 1
    I have improved my answer in particular by adding a second figure giving the discrepancy wrt to a circular arc. – Jean Marie May 18 '25 at 16:00