On the circular embedding of Nguyen Huy Xuong's graph

Question

The following is a conjecture in graph theory.

Circular Embedding Conjecture. Every 2-connected graph has a circular embedding in some surface.

An embedding of a graph in a surface is circular or strong if every face of the embedding is bounded by a cycle of the graph.

Here is a comment from the Wikipedia article on this conjecture:

If a circular embedding exists, it might not be on a surface of minimal genus: Nguyen Huy Xuong described a 2-vertex-connected toroidal graph none of whose circular embeddings lie on a torus.

The graph is, unfortunately, not presented, but I believe it to be the same one in this article from Cantor's Paradise, which I include below together with its introduction

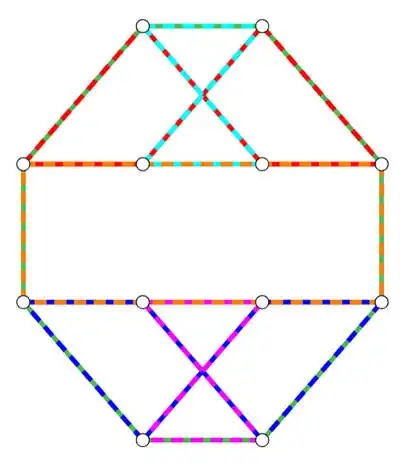
Interestingly, the genus of a graph is not necessarily the same as the genus required for a strong embedding of a graph. The first example discovered of this phenomenon was provided by the mathematician Nguyen Huy Xuong, and is depicted below.

So far so good. Except this graph admits a cycle double cover consisting of $6$ cycles

Accordingly with the second article, the cycles from a cycle double cover of a 2-connected cubic graph, such as Xuong's, should correspond to the faces of some embedding. But Xuong's graph has $12$ vertices and $18$ edges, so $6$ faces gives us an Euler's characteristic of $0$ and thus a genus of $1$, which is the genus of the graph, as shown by the toroidal embedding above. So what is going on here? Even if it is true Xuong's graph does not have a circular embedding on the torus, doesn't it have a circular embedding on another surface of genus $1$, contradicting the claim the genus of the surface is not minimized?

Answer 1

Generally speaking, the genus of a graph is defined to be its orientable genus: the minimum $g$ such that the graph has an embedding in a $g$-holed torus (a sphere, if $g=0$). The graph $G$ in the question (which appears on page III-51 of Xuong's Ph. D. thesis, Sur quelques problèmes d’immersion d’un graphe dans une surface) has no planar embedding, and does have an embedding in the torus, so it has genus $1$; it has no strong embedding in the torus, but does have a strong embedding in the two-holed torus, so it has strong genus $2$.

The double cycle cover in the question gives an embedding of $G$ in the Klein bottle. We can tell because:

• The Euler characteristic is $0$;
• The red and light blue cycles, for example, share two edges, but the orientations are incompatible: no matter how you orient the two cycles, they will follow one of the two shared edges in the same direction and the other in opposite directions. (For an oriented cycle cover, we'd like them to follow all shared edges in opposite directions.) So the surface is non-orientable.

Conventionally, the Klein bottle is said to have non-orientable genus $2$, because it's the connected sum of two projective planes (just like an orientable genus-$2$ surface is the connected sum of two tori). So even if we considered non-orientable genus, we wouldn't say that $G$ has a strong embedding of genus $1$.

If this is not satisfying, Mohar (2010) gives examples of graphs on $18n-6$ vertices with genus $1$ for which every strong embedding (in an orientable or a non-orientable surface!) has genus at least $n$. This forces the Euler characteristic into arbitrarily large negative numbers, as well.