How to formally show these functions are solutions to these ODEs of finite duration? $g''=-\text{sgn}(g')$
Summary: I need to formally demonstrate the following is an equivalence: $$\def\sgn{\operatorname{sgn}} \boxed{- \sgn(g'(0))\cdot\theta\!\left(|g'(0)|-t\right) \overset{?}{\equiv} -\sgn\Biggr(\sgn(g'(0))\left(|g'(0)|-t\right)\cdot\theta\!\left(|g'(0)|-t\right)\Biggr)}$$
Brief Intro
I am trying to understand ODEs of finite duration, so I tried by tackling the easiest examples I found, and so far, I think the following solutions kind of share a similar composition.
The first one I found is in this question, that could be used to "represent the water height in a pierced cylindrical bucket" (this thanks to @ThomasRichard), check the question for details: $$\def\sgn{\operatorname{sgn}} y'=-\sgn(y)\sqrt{|y|} \tag{Eq. 1}\label{Eq. 1}$$ which I think has a finite duration solution: $$y(t) = \frac{\sgn(y(0))}{4}\left(2\sqrt{|y(0)|}-t\right)^2\cdot\theta\!\left(2\sqrt{|y(0)|}-t\right) \tag{Eq. 2}\label{Eq. 2}$$ Where $\theta(t)$ is the Heaviside step function, and $\sgn(x)$ is the Sign function.
In the mentioned question's answer user @Gerd shown that from the initial conditions until the finite extinction time $T = 2\sqrt{|y(0)|} < \infty$ the solutions holds uniqueness, since after it is stitched to the trivial zero solution: it is a singular ODE since is Non-Lipschitz, without this singular point in time it wouldn't be able to stop moving just by itself, as example, nor non-piecewise power series could match a constant value for a non-zero measure interval or it would violate the Identity theorem, so traditional power series method shouldn't work as an accurate description.
Main question
Looking for other examples I found the following, which has been mistakenly solved by me and closed in PhysicsSE such as in MSE: A brick sliding in an horizontal plane after an initial push (under Coulomb's dry friction) - closed form solutions validation? and also here with many downvotes. Later I found I was mistakenly assuming it must stop moving at equilibrium position, so I was missing an integration constant (mentioned by @RollenS.D'Souza in his answer).
Now I think I found the solutions to these ODEs: $$ z'=-\sgn(z) \tag{Eq. 3}\label{Eq. 3}$$ has as finite duration solution: $$z(t) = \sgn(z(0))\cdot\left(|z(0)|-t\right)\cdot\theta\!\left(|z(0)|-t\right) \tag{Eq. 4}\label{Eq. 4}$$ and by integration and some constants manipulation: $$ g''=-\sgn(g') \tag{Eq. 5}\label{Eq. 5}$$ has as finite duration solution: $$g(t) =g(0)+ \frac{\sgn(g'(0))}{2}\cdot\left[|g'(0)|^2-\left(|g'(0)|-t\right)^2\cdot\theta\!\left(|g'(0)|-t\right)\right] \tag{Eq. 6}\label{Eq. 6}$$ which I think are solutions by inspection, but I couldn't formally prove it since there are some issues with their non-linearity: I don't know if/how formally could I move things of the RHS outside the sign function.
I built them to use the fact that $$(f\theta)'=f'\theta+\underbrace{f\delta}_{\equiv\,0\text{ since }x\delta(x)=0}$$ so I built them kind of brute force such its argument make it happen, and also noting from \eqref{Eq. 2} how the first sign function has somehow to complete the initial condition when evaluating at $t=0$.
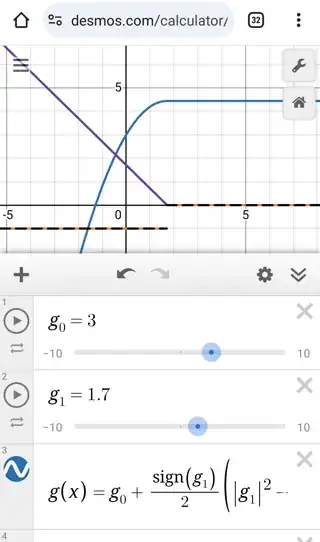
As example, in Desmos looks like it is indeed solving the differential equations.
Motivation
If solution \eqref{Eq. 6} is rightly done, then by considering positive constants $\{k,\,g\}$ then the mentioned system of a brick sliding in an horizontal plane after an initial push under Coulomb's dry friction which has a differential equation with $kg>0$: $$ x''=-kg\,\sgn(x') \tag{Eq. 7}\label{Eq. 7}$$ will have as finite duration solution: $$x(t) =x(0)+ \frac{kg\cdot\sgn(x'(0))}{2}\cdot\left[\left(\frac{|x'(0)|}{kg}\right)^2-\left(\frac{|x'(0)|}{kg}-t\right)^2\cdot\theta\!\left(\frac{|x'(0)|}{kg}-t\right)\right] \tag{Eq. 8}\label{Eq. 8}$$ which would solve my previous questions with only partial answers so far.
Bonus Track (suppressed)
I am asking now how good \eqref{Eq. 8} fit the physics problem in this question on the Physics SE, since there is something that kind of didn't fit.
Added later
Since I don't have yet any answer, I want to show explicitly where I am stuck. By taking the first derivatives of equation \eqref{Eq. 6} I got: $$\begin{array}{r c l} \dfrac{d}{dt}\left(g(t)\right) & = & \require{cancel}\cancel{\dfrac{d}{dt}\left(g(0)\right)}+ \frac{\sgn(g'(0))}{2}\cdot\left[\require{cancel}\cancel{\dfrac{d}{dt}\left(|g'(0)|^2\right)} - \dfrac{d}{dt}\left(\left(|g'(0)|-t\right)^2\cdot\theta\!\left(|g'(0)|-t\right)\right)\right] \\ & = &\frac{\sgn(g'(0))}{2}\cdot\left[-2 \left(|g'(0)|-t\right) \cdot \left(\require{cancel}\cancel{\dfrac{d}{dt}\left(|g'(0)|\right)}-1\right)\cdot\theta\!\left(|g'(0)|-t\right) - \underbrace{\require{cancel}\cancel{\left(|g'(0)|-t\right)^2\cdot\delta\!\left(|g'(0)|-t\right)}}_{=\,0,\,\text{due}\,x^n\delta(x)=0}\right] \\ & = & \frac{\sgn(g'(0))}{\require{cancel}\cancel{2}}\cdot\left[\require{cancel}\cancel{2} \left(|g'(0)|-t\right)\cdot\theta\!\left(|g'(0)|-t\right)\right] \end{array}$$ $$\Rightarrow g'(t) = \sgn(g'(0))\cdot\left(|g'(0)|-t\right)\cdot\theta\!\left(|g'(0)|-t\right)\tag{Eq. 10}\label{Eq. 10}$$ which matches with equation \eqref{Eq. 4}, so far so good. Now taking the derivative again: $$\begin{array}{r c l} \dfrac{d}{dt}\left(g'(t)\right) & = & \sgn(g'(0))\left[\left(\require{cancel}\cancel{\dfrac{d}{dt}\left(|g'(0)|\right)}-1\right)\cdot\theta\!\left(|g'(0)|-t\right) + \underbrace{\require{cancel}\cancel{\left(|g'(0)|-t\right)\cdot\delta\!\left(|g'(0)|-t\right)}}_{=\,0,\,\text{due}\,x^n\delta(x)=0}\right] \\ \end{array}$$ $$\Rightarrow g''(t) = - \sgn(g'(0))\cdot\theta\!\left(|g'(0)|-t\right) \tag{Eq. 11}\label{Eq. 11}$$ So, what I need to demonstrate is that \eqref{Eq. 11} it is equivalent to: $$-\sgn\Biggr(\sgn(g'(0))\cdot\left(|g'(0)|-t\right)\cdot\theta\!\left(|g'(0)|-t\right)\Biggr) \tag{Eq. 12}\label{Eq. 12}$$
$$\boxed{- \sgn(g'(0))\cdot\theta\!\left(|g'(0)|-t\right) \overset{?}{\equiv} -\sgn\Biggr(\sgn(g'(0))\left(|g'(0)|-t\right)\cdot\theta\!\left(|g'(0)|-t\right)\Biggr)}$$
First of all, for $t \geq T$ it could be shown that $g'(t\geq T) = g''(t\geq T) = 0$ since $\theta(T-t\leq 0) = 0$, so \eqref{Eq. 5} is trivially fulfilled as $g'' = 0 \equiv -\sgn(g') = -\sgn(0) = 0$. With this, I can only focus when $t<T$, so I could make expansions like $\sgn(\theta\!\left(|g'(0)|-t\right))=\dfrac{\theta\!\left(|g'(0)|-t\right)}{|\theta\!\left(|g'(0)|-t\right)|}$ without getting into problems because of dividing by zero.
Next, I can expand \eqref{Eq. 12} as: $$\begin{array}{r c l} -\sgn\Biggr(\sgn(g'(0))\cdot\left(|g'(0)|-t\right)\cdot\theta\!\left(|g'(0)|-t\right)\Biggr) & = & -\dfrac{\sgn(g'(0))\cdot\left(|g'(0)|-t\right)\cdot\theta\!\left(|g'(0)|-t\right)}{|\sgn(g'(0))\cdot\left(|g'(0)|-t\right)\cdot\theta\!\left(|g'(0)|-t\right)|} \\ & = & -\dfrac{\sgn(g'(0))\cdot\left(|g'(0)|-t\right)\cdot\theta\!\left(|g'(0)|-t\right)}{|\sgn(g'(0))|\cdot|\left(|g'(0)|-t\right)|\cdot|\theta\!\left(|g'(0)|-t\right)|} \\ & = & -\sgn(g'(0))\cdot\sgn(|g'(0)|-t)\cdot\sgn(\theta\!\left(|g'(0)|-t\right)) \\ & = & g''(t)\cdot\dfrac{\sgn(|g'(0)|-t)}{|\theta\!\left(|g'(0)|-t\right)|} \end{array}$$ Now calling $g'(0):=a\in\mathbb{R}$ I have that the equivalence is tied to the function: $$f(t) = \dfrac{\sgn(|a|-t)}{|\theta\!\left(|a|-t\right)|} = \begin{cases} 1,\quad t<|a|\\ \text{undefinded},\quad \text{otherwise}\end{cases} \tag{Eq. 13}\label{Eq. 13}$$
So I believe $g(t)$ is indeed a solution to \eqref{Eq. 5} before the finite extinction time $t < T = |g'(0)|<\infty$, and since for the times where $t\geq T$ it is fulfilled by the trivial zero solution, so I believe the solution from \eqref{Eq. 6} do solves the differential equation for all times, but I don't know if the presented argument is formally a valid/formal demonstration.
2nd Added later
I think now there is an issue only at time $t=T$: In the scenario of \eqref{Eq. 5} when I evaluate the differential equation with $T=|g'_0|$ then \eqref{Eq. 10} becomes $\operatorname{sgn}(g'(T))=\operatorname{sgn}(0)=0$, but \eqref{Eq. 11} becomes $g''(T)=\operatorname{sgn}(g'_0)\theta(0)\neq 0$, so only on this zero-meassure point the solution it isn't fulfilling the differential equation, but I don't know if it is just an artifact since $g(T)=0$ is already zero: Does the solution of \eqref{Eq. 6} solves \eqref{Eq. 5} for all times?