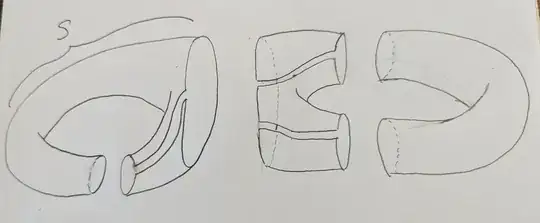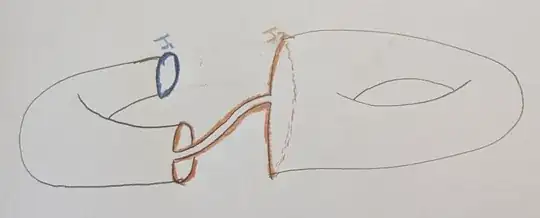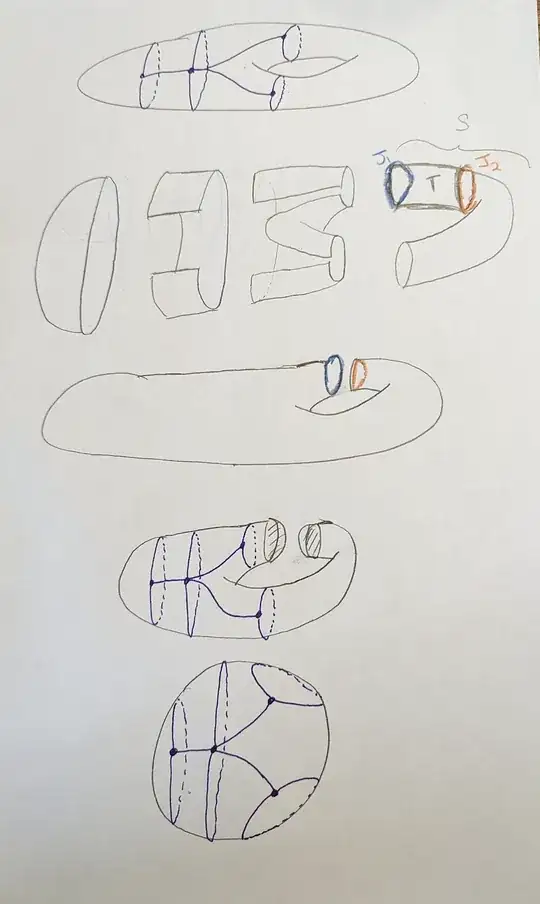A theorem about graph embeddings

Question

I'm trying to learn about graph embeddings and came across a procedure called the "capping operation", as shown in Minimal Imbeddings and the Genus of a Graph and also proved in Monotone Transformations of Two-Dimensional Manifolds. Defining the operation requires first proving the theorems in the figure but I suppose I don't get the intuition on these theorems. I'd appreciate if someone could give a figure on the theorem to explain the application on the theorem. The example I'm trying to see through is the embedding of a triangle on a torus, where the triangle cannot contract to a point. Then the lemma in the figure implies that there should exist a subcomplex $T$ (which as I think, means as a submanifold equipped by a CW-structure) that is a surface with boundary and also components of $S\setminus T$ are all open cylinders but I can't think of such $T$. Another thing I cannot understand is that if there is an example of an embedding where there exists a component $X$ of $X\setminus G(X)$ (where $G(X)$ denotes an embedding of $G$ on $X$) such that $\partial T$ contains more than one component.

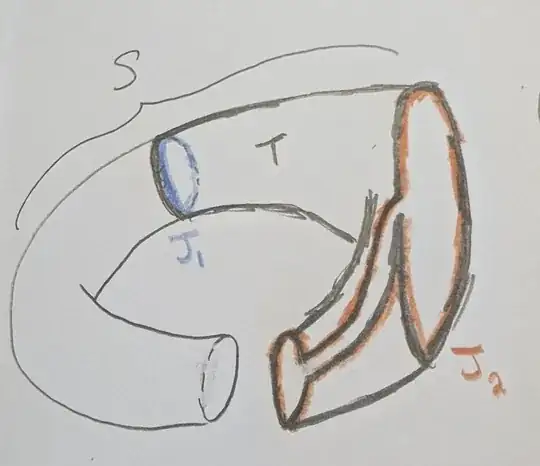
Lemma 4.4. If $G(X)$ is an embedding of a graph $G$ on a surface $X$. Let $S$ be a component of $X \setminus G(X)$. Then $S$ contains a subcomplex $T$ which is a 2-manifold with boundary. More specifically, if $J_1, \ldots, J_s$ where $s \geq 1$ are the Jordan-curves which constitute the boundary of $T$, then

(1) The components of $(S \setminus T)$ are open cylinders ${L_1}, \ldots, {L_s}$

(2) Bd(${L_i}$) has two components, ${J_i}$ and a subset of $G(X)$

Theorem 4.5. Suppose $G(X)$ is an embedding of a graph $G$ in a surface $X$. Let $S$ be a connected component of $X \setminus G(X)$. Let $T, J_1, \ldots, J_s$ and $L_1, \ldots, L_s$ be as in the lemma above. Let $X_S$ be the surface obtained from $X \setminus \text{Int} T$ by connecting the boundary curves $J_i$ with open 2-cells $C_i$. Then the following properties hold.

(1) $G(X)$ is also an embedding $G(X_S)$ of $G$ in $X_S$.

(2) $\chi(X_S) \geq \chi(X)$

(3) $\chi(X_S) = \chi(X)$ if and only if $S$ is an open two-cell. And in this case we may regard $T$ as $S$ and simply let $X_S$ be $X$. All properties will hold properly.

(4) $\lVert X_S \rVert \geq \lVert X \rVert$ and the components of $X_S \setminus G(X_S)$ are open two cells and the components of $X \setminus G(X)$ removing $S$.

A generalization of this statement is mentioned in the following figure, where I am even more lost to the example on torus.

If $M$ is a 2-manifold (which need not be orientable), if $K$ is a non-empty continuum which is a proper subset of $M$, and $S$ is a component of $(M - K)$, then $S$ contains a complex $T$ which is a 2-manifold-with-boundary. Moreover, if $J_1, \ldots, J_s$ $(s \geqq 1)$ are the Jordan curves which constitute the boundary of $T$, then

(1) The components of $(S - T)$ are open cylinders $L_1, \ldots, L_s$

(2) $\text{Fr}(L_i)$, the frontier of $L_i$, has two components, $J_i$ and a subset of $K$, $i = 1,\ldots, s$

Any sketch of an example or further explanation is very much appreciated!

Answer 1

I'm not sure what your first source is, since even the author you're quoting seems to be pretty confused by what's going on... But it might be worth looking for another source, as this might be related to your confusion. Regardless --

The "capping operation" is a way to turn an embedding of a graph $G$ in a surface $X$ into a "2-cell embedding" in a new surface $X'$. Here a "2-cell embedding" means that the complement $X' \setminus G$ is a union of 2-cells (read: open disks), and the operation sending $X$ to $X'$ will only ever reduce the genus (and in fact it will reduce the genus at each step until the algorithm is finished). I think the best way to explain this algorithm is to just draw a bunch of pictures, so let's do that!

We'll start with an embedding of a graph $G$ (shown in purple) in a genus 2 surface:

Then we cut this surface along the graph to get a bunch of pieces, and chose one of our pieces which is not a disk to be $S$.

We choose a big submanifold $T$ of $S$ which leaves behind only cylinders when we remove it, here's one such choice. Note that it has two boundary components, colored in blue and orange. These are the "$J$"s in the statement. The unmarked boundary component, which is in $S$ but not $T$, is our $L_1$. Also, while we're here:

As a fun exercise in visualization, what "simple" surface (with boundary) is $T$ homeomorphic to?

Next we take remove the interior of $T$ from $X$:

and define $X_S$ to be what we get by "capping off" these blue and orange boundary components with disks:

Note that $G$ still embeds in this new surface $X_S$:

Now we can squish things around a little to get a better picture of our new surface, and then we go again. I'll put it all in one picture this time, since we have a better idea of what's happening now:

And of course now, if we tried to do it again, what would happen? We would cut our surface into a bunch of disks! This tells us to stop, since we now have a 2-cell embedding of $G$ into a surface.

---

I hope this helps ^_^