Tic-tac-toe can be certainly won in 2D (on a 2-dimensional square grid including diagonals) already if the field is just slightly larger: 4x4 (while 3x4 still is a draw).
There is an excellent video by 'PBS infinite series' -see references- that looks into longer lines needed in a grid of larger dimensions for the game to be a certain win or draw.
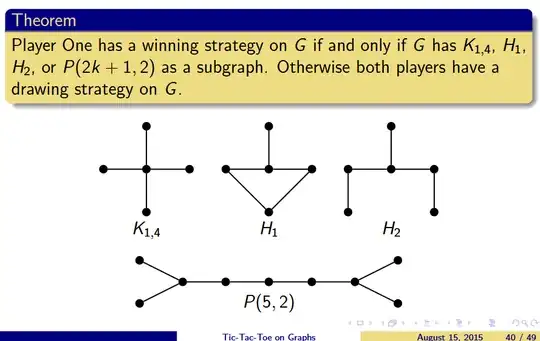
I wonder about tic-tac-toe on a graph: What about $t^3$, 3 adjacent tics or crosses needed, on a simple graph (no loops, no multi-edges)?
What is the condition on the graph for the $t^3$ game (3 adjacent tics needed) to be a certain draw or a certain win?
- On a complete graph with 5 or more vertices, you can always win...
- On a cycle graph, you can always draw
References
- https://www.youtube.com/watch?v=FwJZa-helig
- https://en.wikipedia.org/wiki/Tic-tac-toe aka noughts and crosses or Xs and Os
- Higher Dimenional Tic Tac Toe
- Is there a dimension of tic-tac-toe where there can never be a draw game?
- https://en.wikipedia.org/wiki/Hales%E2%80%93Jewett_theorem
- ///
- A non-losing strategy for tic-tac-toe $\times$ tic-tac-toe
- Winning strategies in multidimensional tic-tac-toe
- Prove that a game of Tic-Tac-Toe played on the torus can never end in a draw. (Graph theoretic solutions only.)
- Which mathematical game or puzzle did you invent?