The shortest period of the sum of $2$ functions with coprime commensurate periods.

Question

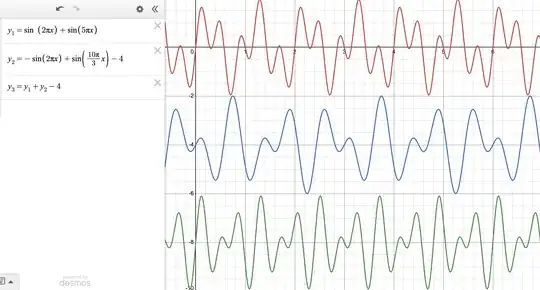
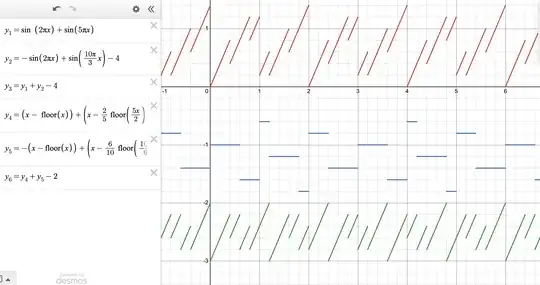
Here is the question: Let $f,g$ be $2$ functions with shortest period $t_1=2$ and $t_2=3$ respectively. Is it true that $h:=f+g$ has shortest period $6$?

My thoughts:

1. It is in general not true that if $t_1,t_2$ are commensurate, then $t:=\mathrm{lcm}(t_1,t_2)$ is the shortest period of $h$. But all the counter-examples I have seen are the case when $t_1=t_2$, for example, $f=\sin x$ and $g=-\sin x$. Are there any counter-examples with $t_1\neq t_2$, even with $\gcd(t_1,t_2)=1$? (related: Period of the sum/product of two functions)

2. If we further add the continuous condition of both $f$ and $g$, then according to The sum of two continuous periodic functions is periodic if and only if the ratio of their periods is rational? $h$ cannot have irrational period, and if it has a shorter rational period $\frac{p}{q}$ with $\gcd(p,q)=1$, then $$ \begin{cases} 3\mid 2p\\ 2\mid 3p \end{cases}\Rightarrow 6\mid p$$ Now $\frac{6r}{q}$ ($\gcd(r,q)=1$) is a period, so as $\frac{6q}{q}$, so as $\frac{6}{q}$. However, is it necessary that $q=1$? Or can we construct counter-examples in this case?

Any comments or solutions are welcomed. Thanks in advance!

Answer 1

As it turns out, the answer is no. Every function involved here has a period (not necessarily shortest) of $6$, so can be expanded (under mild hypotheses) into Fourier series

$$f(x) = \sum f_n e^{\frac{\pi}{3} i n x}$$ $$g(x) = \sum g_n e^{\frac{\pi}{3} i n x}$$ $$h(x) = \sum h_n e^{\frac{\pi}{3} i n x}$$

where $h_n = f_n + g_n$. Given that,

• $f(x)$ has shortest period $2$ iff the $\gcd$ of all $n$ such that $f_n \neq 0$ is $3$, and similarly
• $g(x)$ has shortest period $3$ iff the $\gcd$ of all $n$ such that $g_n \neq 0$ is $2$.

This means there is some odd $a$ such that $f_{3a} \neq 0$ (or else the $\gcd$ would be divisible by $6$), and similarly there is some $b \not \equiv 0 \bmod 3$ such that $g_{2b} \neq 0$ (or else the $\gcd$ would be divisible by $6$). So $3a \neq 2b$, and $g_{3a} = f_{2b} = 0$, meaning that

$$h_{3a} = f_{3a} \neq 0$$ $$h_{2b} = g_{2b} \neq 0.$$

It follows that the $\gcd$ of all $n$ such that $h_n \neq 0$ (which determines the shortest period; if this $\gcd$ is $q$ then the shortest period is $\frac{6}{q}$) is not divisible by $2$ or $3$.

However, this doesn't rule out the possibility that it could be divisible by a larger prime! We can construct an example where $q = 5$ so the shortest period is $\boxed{ \frac{6}{5} }$ as follows. Take

• $h(x)$ to have nonzero coefficients $h_{10}, h_{15}$
• $f(x)$ to have nonzero coefficients $f_{15}, f_6$
• $g(x)$ to have nonzero coefficients $g_{10}, g_6$

where $f_6 = - g_6$, so those coefficients cancel upon addition. So explicitly, and converting to real functions, we can take

$$f(x) = \sin (2 \pi x) + \sin (5 \pi x)$$ $$g(x) = - \sin (2 \pi x) + \sin \left( \frac{10 \pi}{3} x \right)$$ $$h(x) = \sin (5 \pi x) + \sin \left( \frac{10 \pi}{3} x \right)$$

although this way of writing the functions makes it a little harder to tell what their shortest periods are. Here are their graphs in Desmos (translated to make them easier to distinguish) for visual confirmation:

And some alternate graphs that might be easier to understand visually, where $\sin 2 \pi x$ has been replaced with the fractional part $\{ x \} = x - \lfloor x \rfloor$: