I am working on a problem showing that a high-(uniform)-rank, low-dimension tensor of complex numbers can be decomposed into a matrix product state (MPS) and how this process can be parallelised across multiple devices.
The idea is illustrated in the image attached, showing a rank-5 tensor in Penrose 'blob' notation. An SVD is performed between each rank to produce a product of matrices (or a tensor train).
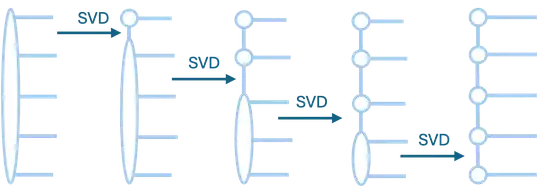
Illustrating SVD decomposition of high-rank tensor to a MPS
If I had high-dimensional ranks the problem of how to parallelise isn't too difficult since I can just divide the tensor into slices, SVD those, and concatenate the results. However the problem is specifically concerned with low-dimension tensors (e.g. dimension 2 or thereabouts) so slicing has a limited amount of scalability and I need to be able to get up to very high ranks ~ 50.
So I wanted to try to shard the tensor across multiple devices so each device can perform some of the SVD in between the ranks. However, the issue is that the last SVD on each shard has to be performed between parts of the tensor that live across two devices, incurring what would surely be a horrific communication overhead (additionally, I'm not too clear on what should be communicated - since the structure of the tensor in between those ranks will have changed?)
I have refrained from adding code so far since this is a conceptual problem, but I am trying to implement this in python using numpy or PyTorch in case anyone wanted to illustrate how they would get parts of this to work.