2

I would like to ask a question regarding my approach to a problem that has been asked on this forum before:

Given $N$ points drawn randomly on the circumference of a circle, what is the probability that they are all within a semicircle?

My Approach

When I saw the $N$ in the problem, I thought to consider cases where $N$ is small and then build up to bigger $N$ (perhaps by observing a pattern of some kind). We are looking for $p_N$, which was what I called the desired probability. So I considered $N = 2$. Of course, $p_2 = 1$ because no matter where the second point is drawn, a semi-circle can be made to contain the two points.

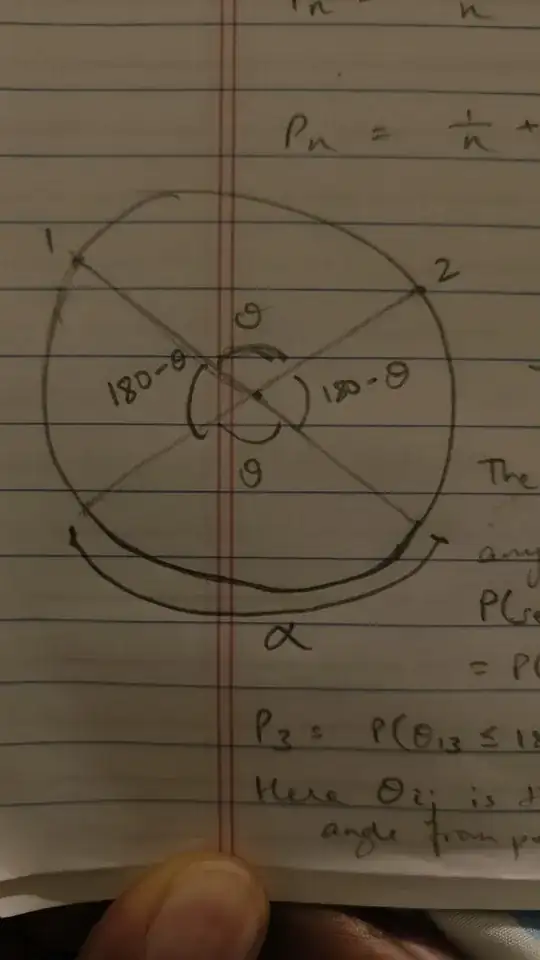
Now, I imagined that two points were already on the circle, and I tried to see how a third point could be placed on the circle such that a semi-circle could be made to contain all three points. Here is the drawing I made:

circle image showing my approach

If the angle spanned by the arc connecting points 1 and 2 is $\theta$, then we can conclude that as long as point 3 is not on the arc directly opposite to that connecting points 1 and 2 - denoted by $\alpha$ in the image - a semicircle can be drawn through all three points.

So $p_3 = p_{2} \times{}P($third point is placed such that semicircle can be constructed$)$. If the angle spanned by the arc connecting points 1 and 2 is $d\theta$, then one minus the second probability is $\frac{Rd\theta}{2\pi R} = \frac{d\theta}{2\pi}$.

$$dP= \frac{d\theta}{2\pi} \implies \int_{0}^{\pi / 2}\frac{d\theta}{2\pi}=\frac{1}{4}$$

$$1 - \frac{1}{4} = \frac{3}{4}$$

My problem is that I have no idea how to go for the $N=4$ case, and I can't even think about generalizing this for any $N$.

Blue
  • 83,939
Abhay Agarwal
  • 335

2 Answers2

4

The best answer to the question has probably already been given (+1). However to specifically address this version of the question and continuing the OP's approach - I think they were building up to an induction argument.

Suppose that when $n$ points are chosen uniformly on a circle, the probability measure for the points lying on a semicircle with largest angle between the points $\theta$ is given by $f_n(\theta)d\theta$, for $\theta\in [0,\pi]$. This leaves a probability of $1-\int_0^{\pi}f_n(\theta)d\theta$ that the points do not lie on a semicircle at all.

Now if we add a new point, the probability measure $f_{n+1}(\theta')d\theta'$ has two components:

  1. The new point lies between the existing points. This contributes $f_n(\theta')\frac{\theta'}{2\pi}d\theta'$ to $f_{n+1}(\theta')d\theta'$. Here $\frac{\theta'}{2\pi}$ is the probability that the new point lies between two points angle $\theta'$ apart.

enter image description here

  1. The new point lies outside the existing points. This contributes $\int_0^{\theta'}f_n(\theta)\frac{2d\theta'}{2\pi}d\theta$ to $f_{n+1}(\theta')d\theta'$. Note the factor of $2$ in the numerator of $\frac{2d\theta'}{2\pi}$ arises because the new point may lie either side of the first $n$ points.

enter image description here

Thus we have:

$$f_{n+1}(\theta')=f_n(\theta')\frac{\theta'}{2\pi}+\int_0^{\theta'}f_n(\theta)\frac{2}{2\pi}d\theta. \qquad (1)$$

We have $$f_2(\theta)=\frac1\pi,\qquad f_3(\theta)=6\left(\frac\theta{2\pi}\right)\frac1{2\pi}, \qquad f_4(\theta)=12\left(\frac\theta{2\pi}\right)^2\frac1{2\pi},\cdots (2)$$

We may prove $$f_n(\theta)=n(n-1)\left(\frac\theta{2\pi}\right)^{n-2}\frac1{2\pi}$$ by induction. By $(2)$ it holds for small values of $n$. Suppose that it holds for some value $n$. Then by $(1)$ we have:

$$f_{n+1}(\theta')= f_n(\theta')\frac{\theta'}{2\pi}+\int_0^{\theta'}f_n(\theta)\frac{2}{2\pi}d\theta\\ =n(n-1)\left(\frac{\theta'}{2\pi}\right)^{n-2}\frac1{2\pi}\frac{\theta'}{2\pi}+\int_0^{\theta'}n(n-1)\left(\frac\theta{2\pi}\right)^{n-2}\frac1{2\pi}\frac{2}{2\pi}d\theta\\ = n(n-1)\left(\frac{\theta'}{2\pi}\right)^{n-1}\frac1{2\pi}+2n\left(\frac{\theta'}{2\pi}\right)^{n-1}\frac1{2\pi}\\=n(n+1)\left(\frac{\theta'}{2\pi}\right)^{n-1}\frac1{2\pi} $$ as required.

Now the probability that all $n$ points lie on a semicircle is $$\int_0^\pi f_n(\theta)d\theta=\int_0^\pi n(n-1)\left(\frac\theta{2\pi}\right)^{n-2}\frac1{2\pi}d\theta=n\left(\frac\pi{2\pi}\right)^{n-1}=n/2^{n-1}.$$

tkf
  • 15,315
  • HI! Thank you so much for your answer. This is what I was looking for. I sincerely apologize for responding so late, but I'm having a little trouble understanding a few things.

    Firstly, since I have not really worked with probability measures directly before, should I interpret $f_{n}(\theta) d\theta$ as the differential change that occurs in the probability of $n$ points lying in a semicircle with largest angle $\theta$ when that largest angle is incremented by $d\theta$?

     – Abhay Agarwal Feb 15 '25 at 01:09
  • Absolutely yes. $f_n(\theta)$ is just the probability density function, so $f_n(\theta)d\theta$ is just the thing that you integrate from $a$ to $b$ to get $P(\theta\in[a,b])$. – tkf Feb 15 '25 at 01:28
  • Hmm, so this is tricky. Maybe this is because I'm not intuitively able to switch from discrete to continuous probability in my head. Here is how I'm trying to understand it:

    Let $P_{n}(\theta)=$ probability that $n$ points fit in a semicircle with largest angle $\theta$

    Then $P_{n+1}(\theta^{'})=P_{n}(\theta^{'})\frac{\theta^{'}}{2\pi} + \int_{\theta=0}^{\theta=\theta^{'}}P_{n}(\theta)\frac{d\theta^{'}}{2\pi}$

    Can I reach your equation from here?

     – Abhay Agarwal Feb 15 '25 at 01:43
  • I think you are missing a factor of $2$ on the second term. This comes from their being two ways of picking the new point, to give largest angle $\theta'$ as indicated in the picture. Otherwise what you have written is the same as what I wrote, with $P(\theta)=f(\theta)d\theta$. Note you must interpret $P$ as a measure, because as a number $P(\theta)$ would just be $0$. – tkf Feb 15 '25 at 01:55
  • To be clear $\int_{\theta=0}^{\theta=\theta'}P_n(\theta)$ is the probability that the largest angle after the first $n$ points is less than $\theta'$. Note there is no $d\theta$ in this integral, as you have it already in your $P_n(\theta)$. Then $\frac{2d\theta'}{2\pi}$ is the probability that the final point puts the largest angle in the interval $[\theta',\theta'+d\theta']$. Multiplying the two terms together gives the probability that the largest angle among all $n+1$ points is in the interval $[\theta',\theta'+d\theta']$ and the last point does not lie between earlier points. – tkf Feb 15 '25 at 13:49
  • Also $P_n(\theta')$ is the probability that the largest angle after $n$ points lies in the interval $[\theta',\theta'+d\theta']$. Then $\frac{\theta'}{2\pi}$ is the probability that the last point lies between the earlier points. Multiplying together gives the probability that the largest angle after $n+1$ points lies in the interval $[\theta',\theta'+d\theta']$ and the last point does lie between earlier points. – tkf Feb 15 '25 at 14:00
  • Adding the two terms then gives the total probability that he largest angle after $n+1$ points lies in the interval $[\theta',\theta'+d\theta']$. This is precisely what your equation says. Finally divide through by $d\theta'$ and let $d\theta'$ tend to zero and you get my equation. – tkf Feb 15 '25 at 14:01
  • Isn't $P_{n}(\theta)$ the probability that after $n$ points, the largest angle is $\theta$? In continuous probability, is this the same thing as the probability that the largest angle after $n$ points lies in the interval $[\theta^{'}, \theta^{'} + d\theta^{'}]$? – Abhay Agarwal Feb 15 '25 at 18:08
  • Sorry, the way I have defined it above, $P_{n}(\theta)$ is the cumulative distribution function, isn't it? The probability that the largest angle after $n$ points is $\leq \theta$, right? – Abhay Agarwal Feb 15 '25 at 18:36
  • The probability that the largest angle is $\theta$ is of course $0$. What you wrote makes sense if you interpret $P_n(\theta)$ as a measure or $1$-form e.g. something which you can integrate over any interval to get the probability of the largest angle lying in that interval. This is the same as $f_n(\theta)d\theta$, where $f$ is the probability density function. Let $C_n(\theta)$ be the cumulative distribution function. Then $f_n(\theta)=\frac{dC_n(\theta)}{d\theta}. – tkf Feb 16 '25 at 07:49
  • To keep things simple here - you could think of the interval $[0,\pi]$ chopped up into intervals of length $d\theta$ and $P_n(\theta)$ is the probability of the largest angle lying in the interval $[\theta,\theta+d\theta]$. Then when you integrate $P_n(\theta')$ you are just summing those probabilities. Then your equation is correct (other than the missing $2$). – tkf Feb 16 '25 at 07:55
  • This makes a lot of sense! Thank you so much! – Abhay Agarwal Feb 16 '25 at 20:45
3

Here is an answer without using integration, starting with $3$ points for explanation, and extending it to $n$ points

  • We take three points $1,2,3$ placed uniformly at random on a circle and without loss of generality, consider point $1$ at a fictitious North, $2$ and $3$ successively clockwise of $1$, and consider only the clockwise semicircle with respect to the fictitious North.
    $\underline{\texttt{[Clarification to a query made earlier}}$]
    We are considering point $1$ as the most counterclockwise point among the $3$ and moving clockwise from point to point, that is why only the clockwise semicircle needs to be considered]

  • The other two points must then lie on a semicircle with $Pr = \frac12\frac12 = \frac14$

  • The same applies if the first point chosen is $2$ or $3$,
    thus P($3$ points lie on a semicircle) $=3\cdot\frac14 = 3\left(\frac12\right)^{3-1} $

  • Extending the same argument to $n$ points, $Pr = n\left(\frac12\right)^{n-1}$

true blue anil
  • 48,250