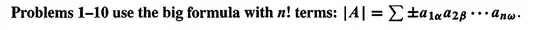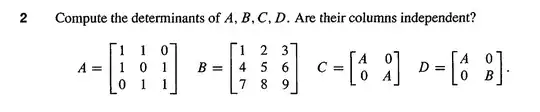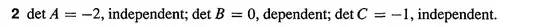This is a question from Gilbert Strang's "Intro to Linear Algebra"
$A$ has 6 permutations but only two of them have non-zero terms, and both these permutations are one row-exchange away from $I$, making the terms negative. Therefore, $\text{det} (A)=-1-1=-2$.
My thought was that the $6\times6$ matrix, given all the zeros, would only have 4 permutations (out of the 720) that had non-zero terms.
$$\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 1 & 0\\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\ \end{bmatrix}\begin{bmatrix} 0 & 1 & 0 & 0 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 1 & 0\\ \end{bmatrix}\begin{bmatrix} 0 & 1 & 0 & 0 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\ \end{bmatrix} $$
Since all four involve two row-exchanges to get to $I$, they would each give a term 0f $+1$, making the determinant equal to $4$. However, the book says the answer is $-1$ and I'm having trouble seeing where this comes from. Did I miss some permutations?