Solve $|3-x| \geq x-5$

Question

$|3-x|= \begin{cases} -3+x, &\text{if x>3} \\ 3-x, &\text{if x $\leq$ 3} \end{cases}$

Consider $x>3:$

$-3+x \geq x-5 \\ -3 \geq -5$

Consider $x \leq 3:$

$3-x \geq x-5 \\ 2x \leq 8 \\ x \leq 4$

In the first case, the variable $x$ got cancelled out. In the second case, the limiting condition is $x \leq 3$, but the calculation yielded $x \leq 4$, so I'm not sure whether $x$ should be non-existent or $x \leq 3$ here.

Regardless the answer is given as $(-\infty, \infty )$. I don't feel my calculations are wrong, so I must have some serious conceptual problems with this type of problem.

Answer 1

You have consider two cases: $x>3$ or $x\le 3$.

For the first case, the statement is always true.

$$\{x:x > 3\} \cap \mathbb{R} =\{x:x> 3\}. $$

For the second case, we started with $x\le 3$: $$\{x:x \le 3\} \cap \{x:x \le 4\} =\{x:x\le 3\}. $$

Taking the union of both cases:

$$\{x:x> 3\} \cup \{x:x\le 3\}=\mathbb{R}.$$

Answer 2

Mind the logical operators "or" and "and": $$\begin{align}|3-x|\ge x-5&\iff[(x>3\text{ and }x-3\ge x-5)\text{ or }(x\le3\text{ and }3-x\ge x-5)]\\&\iff[(x>3\text{ and true})\text{ or }(x\le3\text{ and }x\le4)]\\&\iff[x>3\text{ or }x\le3]\\&\iff\text{true}. \end{align}$$

Alternatively, instead of explicitely splitting into two cases, you can use another definition of the absolute value: $|t|=\max(-t,t)$, and the fact that $\max(u,v)\ge w\iff(u\ge w\text{ or }v\ge w)$: $$\begin{align}|3-x|\ge x-5&\iff\max(x-3,3-x)\ge x-5\\&\iff[x-3\ge x-5]\text{ or }[3-x\ge x-5]\\&\iff[\text{true or }x\le4]\\&\iff\text{true}. \end{align}$$

Answer 3

Since you've already received an answer which addresses your issue, I'll propose a different solution. Note that when $x-5<0$, i.e. when $x<5$, the inequality is always satsfied since the LHS is positive and the RHS is negative. Now consider the case $x\ge 5$; since $|3-x|=|x-3|$, you can solve $|x-3|\ge x-5$. In particular $|x-3|=x-3$ so $|x-3|=x-3\ge x-5$ that is $5\ge 3$. Hence, when $x\ge 5$, the inequality is equivalent to $5\ge 3$, which is always true.

Answer 4

We do not need to consider some cases, such as $\,x\leqslant3\,$ and $\,x>3\,,\,$ indeed , since for any $\,x\in(-\infty,+\infty)\,$ it results that

$|3-x|=|x-3|\geqslant x-3>x-5\;\;,$

we can deduce that the inequality

$|3-x|\geqslant x-5$

is satisfied for all $\,x\in(-\infty,+\infty)\,$ and it means that the solutions of the inequality are all real numbers.

Answer 5

Rewriting:

$|3-x| \ge (x-3)-2$;

$y:=3-x;$

$|y| \ge y-2;$

$1)y \ge 0;$

$y \ge y-2$;

2)$y\lt 0;$

$-y \ge y-2$ or $0\ge - 2;$

Hence $y\in \mathbb{R}$ (Why?)

What follows for $x=3-y?$

Answer 6

Your calculations are correct. Your interpretation is not.

You have case 1. And you have case 2. So the solution was be either a solution to Case 1 OR a solution to case 2.

Each case has an hypotheses and conclusion. SO the solution to each case will be when both hypothesis AND conclusion it true.

In case 1: Your hypothesis is $x > 3$ and your conclusion is $-3 \ge -5$ (which is always true). So the solution to case 1 is when $x > 3$ AND $-3 \ge -5$. That is to say the solution to case 1 is when $x > 3$.

In case 2: Your hypothesis is $x \le 3$ and your conclusion is $x \le 4$. So the solution to case 2 is when $x \le 3$ AND $x \le 4$. $x\le 4$ is a less restrictive instance that is entirely covered by instance $x\le 3$. So the solution to case 2 is when $x \le 3$.

So the complete solution is a solution to Case 1 OR a solution to Case 2.

That is, a solution is when $x < 3$ OR $x \ge 3$. And that occurs.... always.

Evey real number is a solution.

...

But I can see how the logic can be abstract to blinding. Best to do something a bit more direct and hands on that is satisfying to your comfort level of abstraction.

One way, but not the only way, is to not think of unions and intersections but critical points and running tallies.

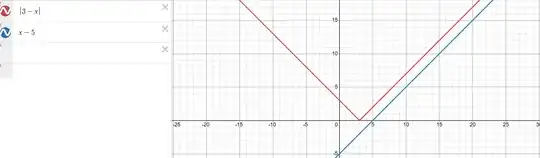
$3-x$ "goes" "from" negative to postive at $x=3$ so consider $x < 3$. Then $|3-x|=3-x \ge x-5\implies x\le 4$ but that's always the case when $x < 3$. So every $x<3$ makes this equation true.

If $x=3$ then $|3-x|=0$ and $x-5=-3$ and obviously $0 \ge -3$ so it's true.

And finally if $x > 3$ then $|3-x| = x-3 \ge x-5\implies -3 \ge -5$ and this is always true.

Putting it together its true when $x < 3$, it's true when $x=3$, and it's true with $x>3$.

So it is always true.

That's the exact same reasoning as above but... maybe a bit more convincing and less abstract.

Answer 7

$$|3-x|\geq x-5$$

$x\leq5$ is clearly in the solution set S of the inequality. For $x>5,$ we can square both sides giving $9-6x\geq -10x+25$ that is $x\geq4.$ So, $x>5$ is also in $S=\Bbb R$.

Another and the quickest way is to look at the graphs of $y=|3-x|$ and $y=x-5.$ The graph of latter is below the former.

Answer 8

Let $x-5=u\Rightarrow x=u+5\Rightarrow |3-x|=|-u-2|=|u+2|$ and thus our initial inequality $$|3-x| \geq x-5$$ becomes $$|u+2|\ge u$$

Now it's easier to see that for $u\lt-2:-u-2\ge u\Rightarrow u\le-1$ which always holds since $u\lt-2$.

while for $u\ge-2: u+2\ge\ u\Rightarrow 2\ge0$ which also always trivialy holds.

Answer 9

You can also see it like this

• for $x\le5$ then $x-5\le 0\le|3-x|$ since an absolute value is always positive

• for $x\ge 5$ then we get $x-3\ge x-5$ which is trivially true

So the inequality is always true.

Answer 10

Plotting the two functions (for example with Desmos) $y_1=f(x)=|3-x|$ (red graph) and $y_2=g(x)=x-5$ (blue graph), you initially can see that the inequality is always true $y_1>y_2, \quad \forall x \in \mathbb{R}=(-\infty,+\infty)=]-\infty,+\infty[$.