Understanding a generalisation of Pòlya's urn (k balls drawn each turn instead of 1)

Question

In interested in a variation on Pòlya's urn. My aim is mostly just to understand its behaviour, but I also want to know whether there's anything special about it, i.e. whether it is in some sense a natural generalisation of the original.

In Pòlya's urn we start with an urn containing $n_0$ black and $m_0$ white balls (the canonical default is $n_0=m_0=1$) and then we repeat the following steps:

• draw one ball from the urn
• duplicate the ball, so if we drew a black ball we now have two black balls, and if we drew white we now have two white balls
• put both balls back into the urn, so it now contains one more ball than it did previously

It's an elementary but fascinating result that, starting with $n_0=m_0=1$, after $T$ time steps, the probability of there being $n$ black balls in the urn is the same for all $1\le n\le T$. In general it converges to a beta distribution.

I'm interested in the following variation. Fix a natural number $k>1$. Then start with $n_0$ black and $m_0$ white balls in the urn where $n_0+m_0\ge k$. On each step,

• draw $k$ balls from the urn (without replacement)
• duplicate all $k$ balls, so if $k=2$ and we drew a black ball and a white ball, we now have two black balls and two white balls
• put all $2k$ balls back into the urn, so it now contains $k$ more balls than it did previously.

I would expect this to behave similarly to Pòlya's urn when the number of balls in the urn is large, because each step will be approximately the same as performing $k$ steps of Pòlya's urn, but when there are small numbers of balls in the urn it will be different.

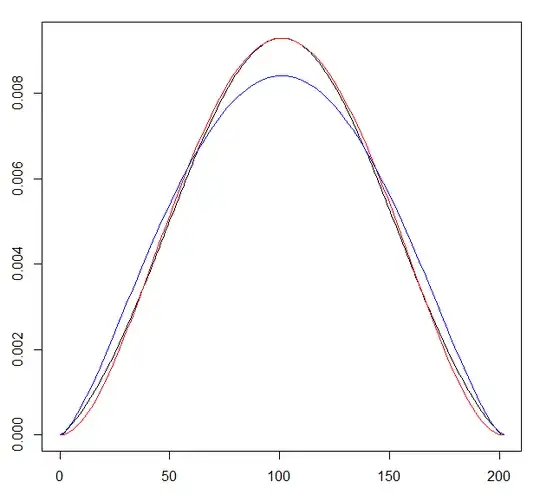
Here is a histogram from simulating the case where $k=2$ and $m_0=n_0=1$, running for 100 time steps.

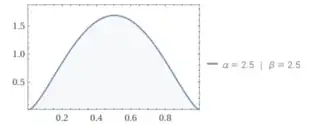
It looks qualitatively similar if I increase or decrease the number of steps. The main question is what distribution this is converging to (as a function of $n_0, m_0$ and $k$). In this case it could plausibly be a beta distribution with parameters at some non-integer value between 2 and 3:

but it could equally be something else.

More generally, I'm interested in whether or not this can be seen as a natural generalisation of Pòlya's urn. That's something of a soft question, but if someone has an intuition for whether we should or shouldn't expect this model to share some of the nice properties that Pòlya's urn has, for example in terms of exchangeability, that would be really useful.

_{(There are many previous questions about variations of Pòlya's urn but I don't think this specific one has been asked about before. Apologies if it has and I missed it.)}

Answer 1

It is not quite a beta distribution. With your example of $100$ draws of $2$ balls starting with $1$ of each, I think $\alpha=3, \beta=3$ gives a reasonable fit for the peak of the distribution (in red below; you also asked about $\alpha=2.5, \beta=2.5$ shown in blue below but it is a worse fit for the peak); the quite good parameters fall slightly with more draws.

Here is some R code which avoids simulation, shown in black below

startgood     <- 1   # at least 1
startbad      <- 1   # at least 0 
draweachtime  <- 2   # no more than startgood + startbad     
numberofdraws <- 100
balls <- startgood + startbad

currentdist <- numeric(balls)
currentdist[startgood] <- 1
for (n in 1:numberofdraws){
  nextdist <- numeric(balls + draweachtime)
  for (d in 0:draweachtime){
    nextdist[(1:balls)+d] <- nextdist[(1:balls)+d] + currentdist * 
                  dhyper(d, 1:balls, (balls-1):0, draweachtime)
    }
  balls <- balls + draweachtime
  currentdist <- nextdist
  }
plot((0:balls), c(0,currentdist), type="l")
curve(dbeta(x/balls,3,3)/balls, from=0, to=balls, col="red", add=TRUE)
curve(dbeta(x/balls,2.5,2.5)/balls, from=0, to=balls, col="blue", add=TRUE)