Verifying the relations of the pure braid group

Question

I'm looking into presentations of the pure braid group Pn (Artins presentation).

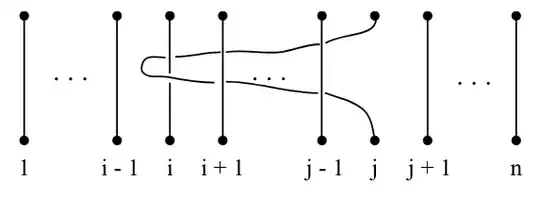
The generator is defined as below:

$A_{i, j} = \sigma _{j-1}\sigma _{j-2}. . .\sigma _{i+1}\sigma _{i}^{2}\sigma _{i+1}^{-1}. . .\sigma _{j-2}^{-1}\sigma _{j-1}^{-1}$

The relations are defined as follows:

$A_{r,s}^{-1}A_{i,j}A_{r,s}=\begin{cases} A_{i,j} & \text{ if }\hspace{1mm}s<i\hspace{1mm}or\hspace{1mm}i<r<s<j\\ A_{r,j}A_{i,j}A_{r,j}^{-1} & \text{ if }\hspace{1mm}s=i\\ A_{r,j}A_{s,j}A_{i,j}A_{s,j}^{-1}A_{r,j}^{-1} & \text{ if }\hspace{1mm}i=r<s<j\\ A_{r,j}A_{s,j}A_{r,j}^{-1}A_{s,j}^{-1}A_{i,j}A_{s,j}A_{r,j}A_{s,j}^{-1}A_{r,j}^{-1} & \text{ if }\hspace{1mm}r<i<s<j \end{cases}$

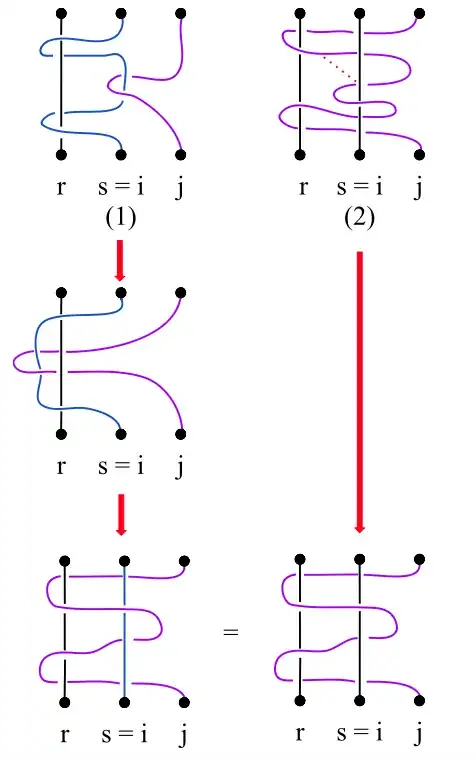
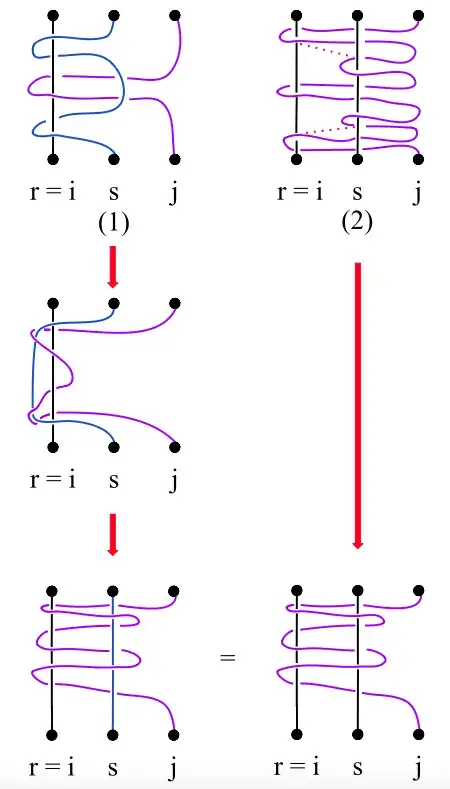
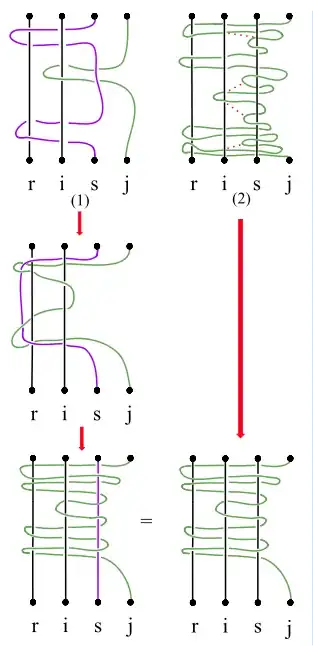
I am having trouble verifying these relations. An intuitive and easy way to do so would be to simply draw the corresponding figures and assure oneself that the braids drawn can be deformed into one another. When I try and draw them, the first relation checks out for both cases, but as for the three remaining relations, something seems to go wrong. I will attach pictures of my attemps at drawing the relations below, and it would be of great help to me if someone could identify what I'm misinterpreting or getting worng.

Here are the two cases of the first relation (these check out):

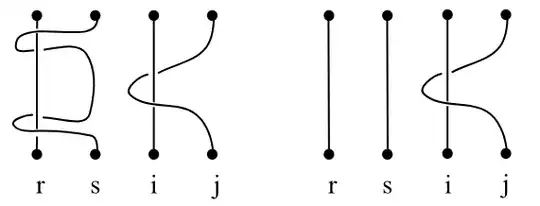
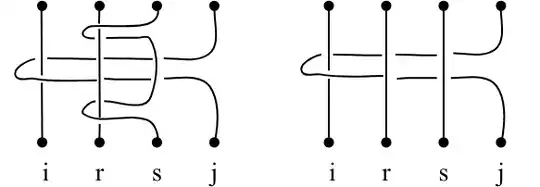
The second relation (something is wrong):

The third relation (something is wrong):

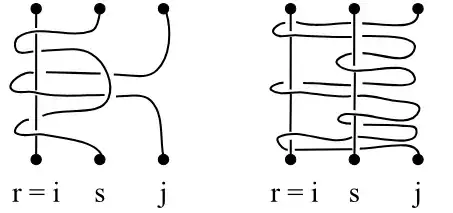
The fourth relation (something is wrong):

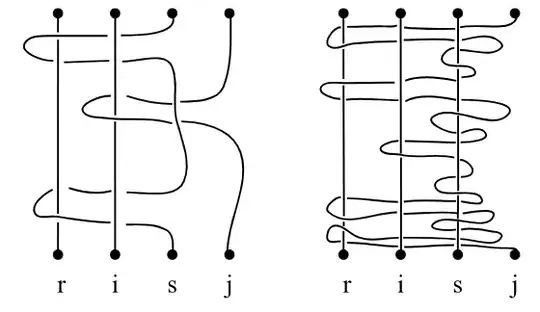
Any input on this or some other way of verifying the relations would be most helpful and very appreciated.

---

Answer 1

Edited to add:

Two pure braids are equivalent if and only if they have the same combing. So one approach would be to "comb" both braids. The process is described nicely in Office Hours with a Geometric Group Theorist, starting on page 391.

Here I have (I think) combed the braids in your $s=i$ relation:

Approach 2:

Here's a sketch of a different approach to verifying the relations (source: chapter 1 of Birman's Braids, Links, and Mapping Class Groups).

I'll use the definition $PB_n = \pi_1(\operatorname{PConf}_n)$.

There is a fiber bundle $$\mathbb{C} - \{p_1, \dots, p_{n-1} \} \hookrightarrow \operatorname{PConf}_n \xrightarrow{f} \operatorname{PConf}_{n-1}$$ where $f$ is "forget the $n$th point," and $f$ has a section $\sigma: \operatorname{PConf}_{n-1} \rightarrow \operatorname{PConf}_n$ given by $$\sigma(p_1, \dots, p_{n-1}) = (p_1, \dots, p_{n-1}, |p_1| + \dots |p_{n-1}| +1). $$

The long exact sequence in homotopy groups of the fiber bundle breaks into split short exact sequences (with splitting $\sigma_*$), and we care about $\pi_1$: $$1 \rightarrow \pi_1(\mathbb{C} - \{p_1, \dots, p_{n-1} \}) \rightarrow \pi_1(\operatorname{PConf}_n) \rightarrow \pi_1(\operatorname{PConf}_{n-1}) \rightarrow 1 $$

This allows us to describe $PB_n = \pi_1(\operatorname{PConf}_n)$ as a semidirect product. Since $\pi_1(\mathbb{C} - \{p_1, \dots, p_{n-1} \}) \cong F_{n-1}$, we get $$PB_n \cong F_{n-1} \rtimes PB_{n-1},$$ and can work out its relations starting with $PB_2 \cong \mathbb{Z}$. So $PB_3 \cong F_2 \rtimes \mathbb{Z}$, ...

Answer 2

Using the approach for continuously deforming ("combing") the braids as suggested by @Chase (in the previous answer), I was able to obtain the following:

(The second relation)

(The third relation)

(The fourth relation)

Wanted to share incase anyone else was looking for drawings like these.