Consider an ellipse centered at the origin with width $2a$ and height $2b$. Choose points $A$, $B$, $C$ independently and uniformly distributed on the perimeter of the ellipse, and create $\triangle ABC$. What is the probability that $\triangle ABC$ is acute given $a$ and $b$?
$\hspace{4.5cm}$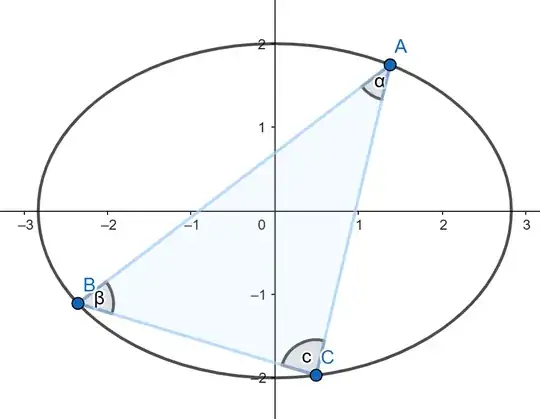
The motivation behind this problem comes from a post discussing Random Triangles Inscribed in Cones and Cylinders. I was interested in the case of a cone, where an inscribed triangle in a cone could also be inscribed in an ellipse.
The case in which $a=b$ (circle) has already been discussed in Probability that the Triangle is Acute. One solution involved parametrizing the three points on a circle, and integrating the three dimensional region described by the constraints of the problem (angles are acute). A solution for the ellipse could possible involve the parametrization $(a\cos\theta_1, b\sin\theta_1), (a\cos\theta_2, b\sin\theta_2), \text{and } (a\cos\theta_3, b\sin\theta_3)$. However, the relationship between $\theta_1, \theta_2, \theta_3$ and the angles of the triangle ($\gamma, \beta, \alpha$) is more complicated in an ellipse than the special case of a cirlce (inscribed angle theorem). This would make it hard to find conditions on $\theta_i$, and be able to integrate on the entire/permissible region.
This post, on how to Generate Random Points on Perimeter of Ellipse provides the method I used to randomly generate a triangle whose vertices lie on the perimeter of an ellipse, and numerically calculate the probabilities for pairs of $a,b$ values. Here is a heatmap of the probability that a randomly inscribed triangle an ellipse of width $2a$ and height $2b$ is acute for $a,b \in (0, 100]$:
I am no expert in coding, so the computations I used were very crude. Nonetheless, here is my python code for the heatmap above. Feel free to adapt this for your own use.
import random
import math
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
code from above source that generates points on ellipse
def ellipse_points(a, b, npoints):
delta_theta=2.0*math.pi/npoints
theta=[0.0]
delta_s=[0.0]
integ_delta_s=[0.0]
integ_delta_s_val=0.0
for iTheta in range(1,npoints+1):
delta_s_val=math.sqrt(a**2*math.sin(iTheta*delta_theta)**2+ \
b**2*math.cos(iTheta*delta_theta)**2)
theta.append(iTheta*delta_theta)
delta_s.append(delta_s_val)
integ_delta_s_val = integ_delta_s_val+delta_s_val*delta_theta
integ_delta_s.append(integ_delta_s_val)
integ_delta_s_norm = []
for iEntry in integ_delta_s:
integ_delta_s_norm.append(iEntry/integ_delta_s[-1]*2.0*math.pi)
ellip_x=[]
ellip_y=[]
ellip_x_prime=[]
ellip_y_prime=[]
npoints_new=40
delta_theta_new=2*math.pi/npoints_new
for theta_index in range(npoints_new):
theta_val = theta_index*delta_theta_new
for lookup_index in range(len(integ_delta_s_norm)):
if theta_val >= integ_delta_s_norm[lookup_index] and theta_val < integ_delta_s_norm[lookup_index+1]:
theta_prime=theta[lookup_index]
break
# ellipse without transformation applied for reference
ellip_x.append(a*math.cos(theta_val))
ellip_y.append(b*math.sin(theta_val))
# ellipse with transformation applied
ellip_x_prime.append(a*math.cos(theta_prime))
ellip_y_prime.append(b*math.sin(theta_prime))
return [ellip_x_prime, ellip_y_prime]
def sideLength(x1, y1, x2, y2):
length = math.sqrt((x2 - x1) ** 2 + (y2 - y1) ** 2)
return length
def acute(lst):
x1 = lst[0]
y1 = lst[1]
x2 = lst[2]
y2 = lst[3]
x3 = lst[4]
y3 = lst[5]
sideAB = sideLength(x1, y1, x2, y2)
sideBC = sideLength(x2, y2, x3, y3)
sideAC = sideLength(x3, y3, x1, y1)
largest = max(sideAB, sideBC, sideAC)
var1 = min(sideAB, sideBC, sideAC)
if sideAB != largest and sideAB != var1:
var2 = sideAB
elif sideBC != largest and sideBC != var1:
var2 = sideBC
else:
var2 = sideAC
if (largest) ** 2 < ((var1) ** 2 + (var2) ** 2):
return True
else:
return False
def prob_acute(a,b, npoints, iterations):
L = ellipse_points(a,b,npoints)
x_coords = L[0]
y_coords = L[1]
valid = 0
for _ in range(iterations):
p1 = random.randint(0, len(x_coords) - 1)
p2 = random.randint(0, len(x_coords) - 1)
p3 = random.randint(0, len(x_coords) - 1)
triangle = [x_coords[p1], y_coords[p1], x_coords[p2], y_coords[p2], x_coords[p3], y_coords[p3]]
if acute(triangle):
valid += 1
return valid/iterations
a_range = np.arange(1, 100, 1)
b_range = np.arange(1, 100, 1)
matrix = np.zeros((len(a_range), len(b_range)))
for i, a in enumerate(a_range):
for j, b in enumerate(b_range):
prob = prob_acute(a,b,1000,10000)
matrix[i, j] = prob
sns.heatmap(matrix, square=True)
plt.xlabel('b value')
plt.ylabel('a value')
plt.title('Probability of Acute Triangle')
plt.gca().invert_yaxis()
plt.show()
Evidently, the probability that an inscribed triangle is acute is the same for ellipses with swapped $a,b$ values, leading to the symmetry. The case of $a=b$ has a $0.25$ chance of being acute, as mentioned in the post linked above. I am hoping the solution is some three dimensional surface to describe the probability for the inputs $a,b$.
Thanks.
