0

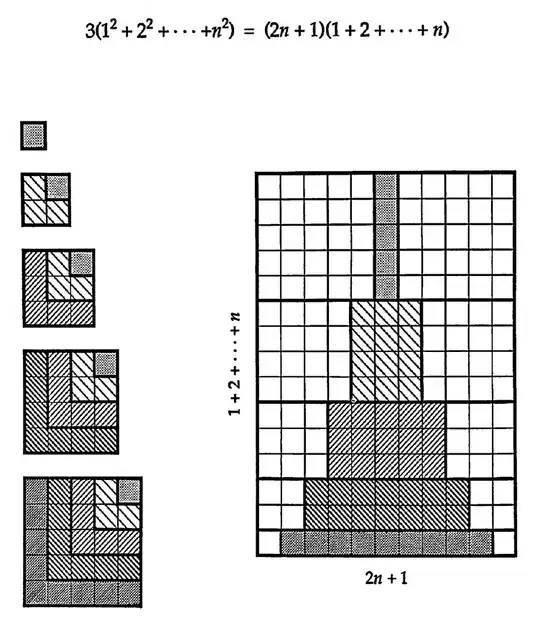
The fact that $$1^2 + 2^2 + \cdots + n^2 = \frac{n(n+1)(2n+1)}{6}$$ can be proven by a straightforward application of mathematical induction involving grinding through a bit of basic high school algebra. But although such a proof does of course suffice to establish that the result is true, it is—like so many proofs by induction—of little value in illuminating why the result is true. And it certainly does not deserve a place in “The Book” of Paul Erdős.

There is also a proof in terms of a telescoping sum, but it too offers little insight into what’s going on.

For such insights, one often turns to combinatorial proofs by double counting or to geometric proofs that provide clear visual understanding. Does either exist in this case?

As for the combinatorial technique—what Ed Scheinerman calls Jeopardy! proofs because one is given the answer(s) and must generate the question—I can cook up a scenario where an unattached man is entertaining $n$ male-female couples, and each person present can choose one of the couples (for example, the couple they think to be the happiest) and one of the men (for example, the one they think to be the wittiest). But that feels like a real stretch, and besides, why on Earth would I want to divide the number of such person-couple-man combinations by 6?

And as for a geometric proof, I can see $n$ squares in the plane strung along the line $y=x$, thus $$[0,1]\times[0,1],\; [1,3]\times[1,3],\; \ldots,\; \left[\frac{n(n-1)}{2}, \frac{n(n+1)}{2}\right]\times \left[\frac{n(n-1)}{2}, \frac{n(n+1)}{2}\right],$$ and considering their total area. But here too I see nothing naturally six about this picture that would induce me to replicate this string-of-squares drawing five more times. Nor do I see any other way to arrange the squares in the plane that’s general enough for all $n\in{\textbf N}^+$. And besides, the right-hand side of the equation is cubic in $n$, so it would seem to call for a picture in ${\textbf R}^3$ rather than ${\textbf R}^2$.

Bill Dubuque
  • 282,220
Paul Tanenbaum
  • 2,622
  • Yes a double counting proof certainly exists and should be around somewhere on this site. For any $n$ consider the number of integer tuples $(x,y,z)$ with $1 \leq x,y\leq z\leq n$. If one fixes $z$, the number of such tuples with precisely this $z$ is $z^2$, so letting $z$ vary gives the number of tuples as $\sum_{i=1}^n i^2$. There is another way to count this set which leads to the answer in terms of a linear sum of binomials. – Sarvesh Ravichandran Iyer Dec 14 '24 at 20:41
  • 1
    In fact, here is the proof I was talking about. – Sarvesh Ravichandran Iyer Dec 14 '24 at 20:44
  • 4
    This question has been asked countless times on this site. For example, here is a link to $32$ answers, including combinatorial and geometrical proofs. Please look for duplicates before asking a question. – anankElpis Dec 14 '24 at 21:10
  • @anankElpis, for the record, I did look, though clearly not assiduously enough. Though it seemed to me unlikely that I was the first, I found no others. – Paul Tanenbaum Dec 14 '24 at 22:45

1 Answers1

0

There are a lot of geometric proofs of this result. From the book "proof without words", I will show two of them here: 1st proof: enter image description here 2nd proof: enter image description here

Sam
  • 3,763