How can I determine if a vector is pointing inwards or outwards a surface?

Question

Let $\gamma:\left[0, \frac\pi2\right] \to \mathbb{R^2}$ be a curve defined by $\gamma(\theta) = (\cos^2(\theta) \sin(\theta) , \cos(\theta) \sin^2(\theta))$.

The following is the image of $\gamma$: 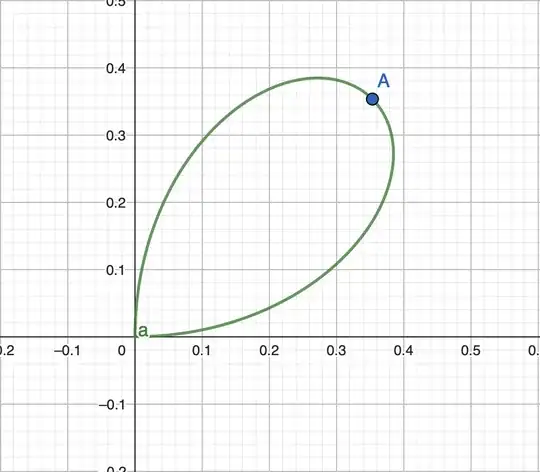where I have labeled $A=\left(\frac{\sqrt2}{4},\frac{\sqrt2}{4}\right)=\gamma\left(\frac{\pi}{4}\right).$

Since I am not confident with the English words used for this mathematical object, let me clarify that we call flux of $F$ through $S$ in the direction of the unit vector $n$ the integral $\int_S (F\cdot n)d\sigma$, where $$\int_S f d\sigma \stackrel{\Delta}{=} \iint_D f(\phi(u,v)) \|\phi_u(u,v) \times \phi_v(u,v)\| du dv.$$ If $S$ encloses a (bounded) region of the space, we say that the flux points inwards or outwards $S$ depending on whether the normal unit vector points towards the region enclosed by $S$ or not.

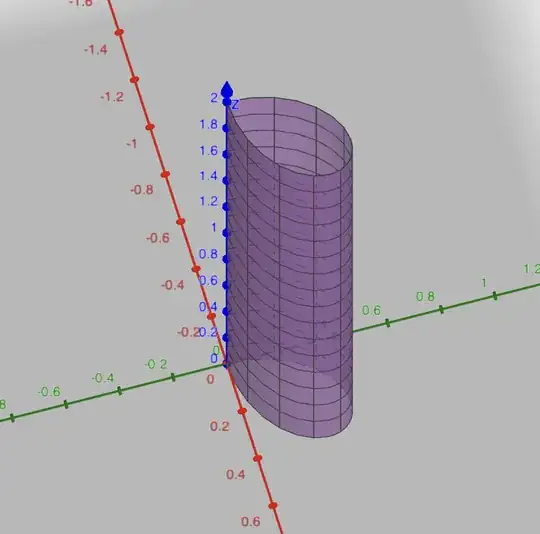
An example in an Italian book that I am studying (by N. Fusco - P. Marcellini - C. Sbordone) evaluates the inward flux of $F(x,y,z)=\left(\sqrt{x^2+y^2},0,z^2\right)$ through the lateral surface of the "cylinder" $S$ whose base is the region enclosed by $\gamma$, height is $2$ and is placed in $H=\{(x,y,z) \in \mathbb{R^3}: z \geq 0\}$.

First, we define $\phi: \left[0, \frac\pi2\right] \times \left[0, 2\right] \to \mathbb{R^3}$ such that $\phi(u,v) = (\cos^2(u) \sin(u) , \cos(u) \sin^2(u), v)$ and find that $\phi_u(u,v) = (\cos^3(u) - 2 \sin^2(u) \cos(u), 2 \sin(u)\cos^2(u) - \sin^3(u), 0)$ and $\phi_v(u,v) = (0,0,1)$. Therefore $\phi_u(u,v) \times \phi_v(u,v) = (2 \sin(u) \cos^2(u) - \sin^3(u), -\cos^3(u) + 2 \sin^2(u)\cos(u), 0).$

Then, the authors of my book observe that the normal vector to the surface in the points $\left(\frac{\pi}{4},v\right)$ is $N(u,v) = \phi_u\left(\frac{\pi}{4},v\right) \times \phi_v\left(\frac{\pi}{4},v\right) = \left(\frac{\sqrt2}{4},\frac{\sqrt2}{4} , 0\right) \implies \hat n(u,v) = \left(\frac{\sqrt2}{2},\frac{\sqrt2}{2} , 0\right)$ and claim that therefore the normal unit vector points outwards $S$, so that the desired flux is actually $\int_S (F\cdot (-\hat n))d\sigma$.

I do not understand how to establish whether the normal unit vector points towards inside or outside $S$. I am not sure if the authors' claim was based on some facts which currently I am unable to get or rather on the picture of the cylinder. If this is the case, I would appreciate a detailed explanation on why the drawing is enough to deduce the direction of the normal unit vector.

However, I wonder how one would deal with a more difficult curve $\gamma$: suppose you cannot draw it. How would you figure out whether the normal unit vector points inwards or outwards?

Answer 1

If you look at the point $A$ in your original drawing, the vector $\hat{n}(u, v)$ (for $u = \pi/4$) points in the direction up-and-to-the-right. That's an arrow into the unbounded component of the complement of the image of your curve, hence outward pointing.

Doing this in general if you can't plot the curve is is a little tricky for curves with corners like yours. Let's assume that at every corner, you temporarily "round off" the corner by replacing it with a small arc of a circle. Furthermore, if necessary reparameterize so that $\| \gamma'(t) \| \ne 0$ everywhere.

Once you've done that, and have a $C^1$ curve, you can compute the turning number of the tangent vector to the curve. Because it's a simple closed curve (otherwise inside and outside are more or less meaningless), the turning number will be $\pm 1$. If it's $-1$, then reverse the orientation of the curve, i.e., replace $\gamma$ with $\alpha(t) =\gamma(\frac{\pi}{2} - t)$. So we can now assume we have a curve with turning number $+1$.

Pick a point $P = \gamma(c)$ for some $c$ in the domain, and let $v = \gamma'(c)$. Then the inward normal direction is $v^\perp$, where this is defined by $$ \pmatrix{a\\b}^\perp = \pmatrix{-b\\a} $$ which is an operation that rotates a vector 90 degrees counterclockwise. (To get the unit inward normal, you'll need to divide by length.)

In practice, the plot and draw approach is much preferred if it's feasible.

Post-comment addition:

If you have a closed $C^1$ curve $\alpha: [a, b] \to \mathbb R^2$ with everywhere nonzero velocity vector $\alpha'(t)$, then $\alpha': [a, b] \to \mathbb R^2$ is also a curve in the plane (albeit only $C^0$). Because this curve never hits the point $(0,0)$, it makes sense to compute the winding number of $\alpha'$ around the point $(0,0)$. This is called the "turning number" for $\alpha$.

If you look for the original paper of Whitney about the Whitney-Graustein theorem, you can see more details. But as an example, if we look at $$ u(t) = (1 + \cos t, \sin t) $$ for $0 \le t \le 2\pi$, then $$ u'(t) = (-\sin t, \cos t) $$ is an everywhere nonzero curve in the plane. Indeed, it describes a unit circle traversed counterclockwise, starting at $(0, 1)$. So its winding number around the origin is $+1$. And thus $u$ has a turning number of $+1$.

Answer 2

Let's define a family of closed surfaces indexed by $t$,

$$\Psi(u, v, t) = t \phi(u, v)$$

The 'surface' described by $\Psi(u, v, 0)$ encloses zero volume as it has been contracted to a single point at the origin, the surface described by $\Psi(u, v, 1)$ is the same surface as $\phi(u, v)$ and encloses some positive volume. Let's call the enclosed volume of the $t$-th surface $V(t)$, the fundamental theorem of calculus then tells us,

$$V(1) - V(0) = V(1) = \int^1_0 \frac{dV}{dt}(t)dt$$

The derivative of the enclosed volume with respect to $t$ can be found by examining the rate at which each infinitesimal area of the surface is sweeping out signed volume as $t$ increases. Each infinitesimal parallelogram is described by a normal vector,

$$\frac{\partial \Psi}{\partial u}(u, v, t) \times \frac{\partial \Psi}{\partial v}(u, v, t) dudv$$

Whose magnitude is the infinitesimal area of the parallelogram and whose direction is either into or out of the surface, let's assume for that moment that it points outwards. As $t$ increases this parallelogram moves with a velocity,

$$\frac{\partial \Psi}{\partial t}(u, v, t)$$

Sweeping out signed volume at the rate,

$$\frac{\partial \Psi}{\partial t}(u, v, t) \cdot \left( \frac{\partial \Psi}{\partial u}(u, v, t) \times \frac{\partial \Psi}{\partial v}(u, v, t) \right) dudv$$

If $\frac{\partial \Psi}{\partial t}$ points outwards this quantity is positive, as the surface is expanding outwards at this location and gaining volume, if it points inwards then this quantity is negative, as the surface is contracting inwards at this location and losing volume. The derivative of the enclosed volume with respect to $t$ is then this quantity integrated over the entire surface,

$$\frac{dV}{dt}(t) = \iint_U \frac{\partial \Psi}{\partial t}(u, v, t) \cdot \left( \frac{\partial \Psi}{\partial u}(u, v, t) \times \frac{\partial \Psi}{\partial v}(u, v, t) \right) dudv$$

$$= t^2 \iint_U \phi(u, v) \cdot \left( \frac{\partial \phi}{\partial u}(u, v) \times \frac{\partial \phi}{\partial v}(u, v) \right) dudv$$

Integrating from $t = 0$ to $t = 1$ gives us the volume enclosed by the original surface,

$$V(1) = \frac{1}{3} \iint_U \phi(u, v) \cdot \left( \frac{\partial \phi}{\partial u}(u, v) \times \frac{\partial \phi}{\partial v}(u, v) \right) dudv$$

If our assumption that $\frac{\partial \Psi}{\partial u} \times \frac{\partial \Psi}{\partial v}$ pointed outwards was wrong, then this would instead give us the negative of that volume. So compute that surface integral, if it's positive then $\frac{\partial \phi}{\partial u} \times \frac{\partial \phi}{\partial v}$ points outwards, if it's negative then it points inwards.

Edit: I realized your construction does not result in closed surfaces which means this method won't work as is, but scaling down by a dimension and repeating essentially the same logic you arrive at an integral for either the positive or negative area enclosed by the curve $\gamma$,

$$\frac{1}{2}\int^b_a \gamma(\theta) \times \frac{d \gamma}{d \theta}(\theta) d\theta$$

Where $\times$ is the 2d scalar-valued cross product. This integral is positive when $\gamma$ wraps counter-clockwise around the enclosed area. Defining,

$$\tilde \gamma(u) = \gamma_x (u) \hat i + \gamma_y (u) \hat j + 0 \hat k$$

and assuming $\gamma$ does wrap counter-clockwise around the enclosed area, then $\frac{d \tilde \gamma}{du} \times \hat k$ points outwards, as this turns the vector 90 degrees clockwise. We then have,

$$\phi(u,v) = \tilde \gamma(u) + v \hat k$$

$$\frac{\partial \phi}{\partial u}(u, v) = \frac{d \tilde \gamma}{du}(u)$$

$$\frac{\partial \phi}{\partial v}(u, v) = \hat k$$

$$\frac{\partial \phi}{\partial u}(u, v) \times \frac{\partial \phi}{\partial v}(u, v) = \frac{d \tilde \gamma}{du}(u) \times \hat k$$

Which we established points outwards. If our assumption was wrong then this will point inwards which will be indicated by the integral evaluating to a negative value.