4

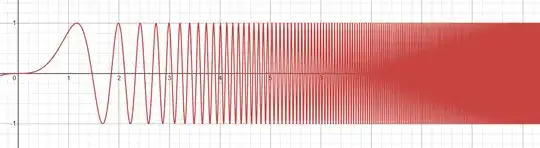
I'm sure there's a better way to describe this, but after some brief searching, I couldn't turn anything up. I'm interested in if there's a way to measure or quantify the "density" of a function. To illustrate what I mean, consider the function $\sin(x^3)$, which has the following plot.

A plot of sin(x^3)

You can clearly see that as $x$ increases, the lines become closer together, causing the function to appear more "dense."

Is there a way to measure this "density?" For example, some way to quantitatively show that for $0<x<1, \sin(x^3)$ is less dense than for $9<x<10$? Is there a better term for what I'm describing?

I had the thought that you could find the arc length of the function over a given domain, but that would only work for oscillatory functions (i.e. that have finite arc length) and not for something that has asymptotic behavior like $\tan(x^3)$.

Edit: To be clear, I don't have a good definition for what I'm meaning here, which is part of the reason for posting the question. But I feel it is fairly intuitive to have some notion that, for the example I gave, the function appears more "dense" as $x$ increases, because the lines are drawn closer and closer together.

YaGoi Root
  • 77
  • 3
    The arc-length idea is a good one, and it can still work for functions with asymptotes if one introduces a cutoff bound $B>0$, and replaces $f(x)$ with $B$ if $f(x)>B$ and replaces $f(x)$ with $-B$ if $f(x)<-B$. – Greg Martin Dec 09 '24 at 17:32
  • @GregMartin That had occurred to me, and for any example that I can think of, it certainly seems to work. However, I confess that it doesn't seem a 'general' approach, as it requires knowledge of an appropriate $B$. It also seems possible to me that there could be cases where the appropriate value of $B$ would vary with $x$, and so $B$ would need to change depending on what domains you were trying to compare. – YaGoi Root Dec 09 '24 at 17:54
  • 1
    The $B$ idea is related to clipping. Another way to convert $f$ into something bounded is to apply a sigmoid function. – Karl Dec 09 '24 at 20:31
  • 1
    On an interval $I = [a,b]$ you could take the density to be the arclength of $f$ over that interval divided by the area of the bounding box: $(b-a)(\max_{x \in A} f(x) - \min_{x \in A} f(x))$. – Jair Taylor Dec 09 '24 at 20:38
  • 1
    To me, it is not clear what is meant by "dense". Why is it not up to OP to determine what they mean by "dense" rather than leave the audience guessing? – Adam Rubinson Dec 09 '24 at 20:46
  • 1
    Jair's idea doesn't help with unbounded functions, but you could modify it by taking the supremum of $\frac{\text{arc length in the box}}{\text{area of the box}}$ over all possible choices of finite upper and lower bounds. – Karl Dec 09 '24 at 20:56
  • 1
    @YaGoiRoot One can compare different intervals' "$B$-clipped" density and then take the limit as $B\to\infty$. – Greg Martin Dec 09 '24 at 21:29
  • @AdamRubinson TBH I'm not sure a good definition of what I've attempted to describe, which is part of the reason for the question. That said, it is intuitive to me, and I'm guessing at least some others as well based on the comments, that, for the example given, as $x$ increases, the fact that the lines of the plot are drawn closer and closer together lends to there being some notion of the function appearing more 'dense,' for lack of a better term. – YaGoi Root Dec 09 '24 at 22:42
  • 1
    The suggestion to use arc length and deal with unbounded functions by taking the limit of a "clipped density" makes a lot of sense. It will be hard for us to offer anything more conclusive without knowing more about what you're trying to do. – Karl Dec 09 '24 at 22:48
  • @Karl I agree, that does seem to be the most practical method. – YaGoi Root Dec 09 '24 at 22:54
  • Perhaps worth mentioning here is that there exist functions $f:\mathbb R \rightarrow \mathbb R$ whose graphs are dense subsets of ${\mathbb R}^2$ (i.e. their graphs approach arbitrarily closely every point in the plane). For examples, see here and here and here and here. – Dave L. Renfro Dec 10 '24 at 02:17

0 Answers0