How to tell which picture is closest to another picture?

Question

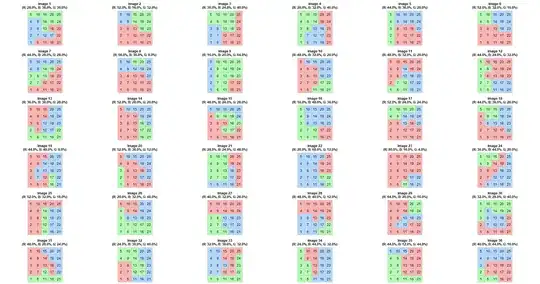
Using a computer, I made the following simulation of 36 random images:

I have the following question: If we take first image as the reference: Which of these other 35 images is the "most similar" to image 1?

I thought about this question for a while and it seems there are 2 ways to measure similarity:

Metric 1: Similarity in terms of color distribution, e.g. (33,33,34) is closer to (30,30,40) compared to (99,1,0). I think something like this can be done with the Euclidean Distance?
Metric 2: Similarity in terms of color positioning: e.g. to compare (image i vs image j), take square k ... if both share the same color then 1 else 0. Do for all squares and measure the percent similarity (I think this is a form of Hamming Distance https://en.wikipedia.org/wiki/Hamming_distance ?)

How can I measure similarity between these all images and image 1?

Reference questions:

Measuring the change in cookie distributions?

In case someone is actually interested, here is the data for the simulations:

[[1]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    2    2    2    2    3
[2,]    1    2    2    2    3
[3,]    1    2    3    3    3
[4,]    1    2    1    3    3
[5,]    1    1    1    3    3
[[2]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    1    1    2    2
[2,]    1    1    1    2    2
[3,]    1    1    1    3    3
[4,]    1    1    3    3    3
[5,]    1    1    3    3    3
[[3]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    2    2    2    3    3
[2,]    2    2    2    3    3
[3,]    1    1    3    3    3
[4,]    1    1    3    3    3
[5,]    1    1    1    1    1
[[4]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    3    3    3    3    3
[2,]    2    2    3    3    3
[3,]    2    2    2    3    3
[4,]    2    2    2    1    1
[5,]    1    1    1    1    1
[[5]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    3    3    3    3    3
[2,]    1    1    1    2    2
[3,]    1    1    1    2    2
[4,]    1    1    1    2    2
[5,]    1    1    2    2    2
[[6]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    1    1    3    3
[2,]    1    1    1    3    3
[3,]    1    1    1    2    2
[4,]    1    1    2    2    2
[5,]    1    1    2    2    2
[[7]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    3    3    2    2
[2,]    1    3    3    2    2
[3,]    1    1    3    3    2
[4,]    1    1    1    3    2
[5,]    1    1    1    1    2
[[8]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    1    1    2    2
[2,]    1    1    1    2    2
[3,]    1    1    1    2    3
[4,]    1    1    1    2    3
[5,]    1    1    2    2    2
[[9]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    2    2    2    2    2
[2,]    3    3    3    3    3
[3,]    3    3    3    3    3
[4,]    1    1    3    3    3
[5,]    1    1    3    3    3
[[10]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    1    1    1    1
[2,]    1    1    1    1    2
[3,]    3    1    1    1    2
[4,]    3    3    2    2    2
[5,]    3    3    2    2    2
[[11]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    3    1    1    1    1
[2,]    3    3    1    1    1
[3,]    3    3    2    2    1
[4,]    2    2    2    1    1
[5,]    2    2    2    1    1
[[12]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    3    3    3    3    3
[2,]    3    3    1    3    1
[3,]    2    2    1    1    1
[4,]    2    2    1    1    1
[5,]    2    2    1    1    1
[[13]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    3    3    1    1    1
[2,]    3    1    1    1    1
[3,]    3    2    2    1    1
[4,]    3    2    2    2    2
[5,]    3    3    2    2    2
[[14]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    1    1    1    1
[2,]    1    1    1    1    2
[3,]    1    1    1    1    2
[4,]    3    3    3    2    2
[5,]    3    3    2    2    2
[[15]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    1    1    1    2
[2,]    1    1    1    3    2
[3,]    1    3    1    3    2
[4,]    1    3    3    3    2
[5,]    1    1    3    2    2
[[16]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    3    3    3    3    3
[2,]    3    3    2    2    2
[3,]    3    3    2    2    2
[4,]    1    1    2    2    2
[5,]    1    1    2    2    2
[[17]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    1    1    3    3
[2,]    1    1    1    3    3
[3,]    1    1    2    2    3
[4,]    1    1    1    2    3
[5,]    1    1    2    2    2
[[18]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    1    1    1    3
[2,]    1    1    2    3    3
[3,]    1    1    2    3    3
[4,]    1    1    2    2    2
[5,]    1    2    2    2    2
[[19]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    1    1    1    1
[2,]    1    2    2    1    1
[3,]    1    1    2    2    1
[4,]    3    3    2    2    2
[5,]    2    2    2    2    2
[[20]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    3    3    3    1    1
[2,]    1    1    1    1    2
[3,]    1    1    1    1    2
[4,]    1    2    1    2    2
[5,]    1    2    2    2    2
[[21]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    2    3    3    3    3
[2,]    2    3    3    3    3
[3,]    2    3    3    3    3
[4,]    2    2    2    1    1
[5,]    1    1    1    1    1
[[22]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    2    2    2    2    2
[2,]    2    2    2    2    2
[3,]    2    2    2    2    2
[4,]    2    3    1    1    2
[5,]    3    3    1    1    1
[[23]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    1    1    1    1
[2,]    1    1    1    1    1
[3,]    3    1    1    1    1
[4,]    2    2    1    1    1
[5,]    2    2    1    1    1
[[24]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    1    1    3    3
[2,]    2    1    1    3    3
[3,]    2    2    1    1    3
[4,]    2    2    2    1    1
[5,]    2    2    2    2    2
[[25]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    1    1    1    1
[2,]    1    1    1    1    1
[3,]    3    3    3    3    1
[4,]    2    2    2    2    1
[5,]    2    2    2    2    1
[[26]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    3    3    3    3    1
[2,]    3    3    2    1    1
[3,]    3    3    2    1    1
[4,]    3    3    2    2    2
[5,]    3    3    2    2    2
[[27]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    3    3    3    1    1
[2,]    3    3    3    1    1
[3,]    3    2    2    1    1
[4,]    2    2    2    1    1
[5,]    2    2    2    1    1
[[28]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    2    2    2    1    1
[2,]    2    2    2    1    1
[3,]    2    2    1    1    1
[4,]    3    2    2    1    1
[5,]    3    3    1    1    1
[[29]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    1    1    1    1
[2,]    1    2    1    1    1
[3,]    1    2    2    1    1
[4,]    1    1    2    3    3
[5,]    1    1    2    3    3
[[30]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    1    3    3    3
[2,]    1    2    2    2    3
[3,]    1    2    2    3    3
[4,]    1    2    2    3    3
[5,]    1    1    1    3    3
[[31]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    3    1    1    1    1
[2,]    3    1    1    1    1
[3,]    3    3    1    1    2
[4,]    3    1    1    2    2
[5,]    3    2    2    2    2
[[32]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    1    1    3    3
[2,]    1    1    1    3    3
[3,]    2    3    3    3    3
[4,]    2    3    3    2    2
[5,]    2    2    2    2    2
[[33]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    3    2    2    2    2
[2,]    3    2    2    2    2
[3,]    3    1    2    1    1
[4,]    3    1    1    1    1
[5,]    3    3    3    3    1
[[34]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    3    3    3    3    3
[2,]    3    3    3    1    1
[3,]    2    1    1    1    1
[4,]    2    2    2    2    2
[5,]    2    2    2    2    2
[[35]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    3    3    3    3    2
[2,]    3    3    3    3    2
[3,]    3    1    1    1    2
[4,]    3    1    1    1    1
[5,]    3    1    1    1    1
[[36]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    3    3    2    2    2
[2,]    3    1    1    2    2
[3,]    3    1    1    2    2
[4,]    1    1    1    2    2
[5,]    1    1    1    2    2

Which metric depends on what you want the metric to measure - how you want to measure distance. You don't give us much to latch onto to make a choice there. — Thomas Andrews, Dec 01 '24 at 04:07
This question is good motivation to explore techniques in computer vision. Accounting for rotations, scalings, local similarity, etc. — A rural reader, Dec 01 '24 at 04:32
@Thomas Andrews: What other metrics apart from distance could we measure? — farrow90, Dec 01 '24 at 04:45
"What other metrics apart from distance could we measure?" -- the answer depends on your idea of what being "close to" means in your problem — rych, Dec 01 '24 at 10:51

rych · Answer 1 · 2024-12-02T02:05:27.517

0

You can view this as 5x5 matrices with $a_{ij}\in \{0,1,2\}$ where 0 encodes blue, 1 - green, 2 - red. Use one of the distances from this answer, for example: $$d_1(A, B) = \sum_{i=1}^n \sum_{j=1}^n |a_{ij} - b_{ij}|$$ and find $\min_B d(A,B)$

However, as @MJD commented, we'd have "the difference between red and blue is twice as big as the difference between red and green". Therefore, instead of $|\cdot|$, let's use one of the functions from What formula returns either a 1 or 0 depending on whether you input any non-zero integer or 0 respectively? For example, $$d_s(A, B) = \sum_{i=1}^n \sum_{j=1}^n |\text{sgn}(a_{ij} - b_{ij})|$$

edited Dec 02 '24 at 02:05

answered Dec 01 '24 at 10:40

rych

4,445

1

Notice that this says that the difference between red and blue is twice as big as tbe difference between red and green, and the difference between blue and green is equal to the difference between red and green. This may be what you want, or perhaps not. – MJD Dec 01 '24 at 18:17
@MJD oh that's right :) Will add this to my post. Thanks! – rych Dec 02 '24 at 02:00
1

thank you for your answer rych! I dont know why you were downvoted and my question was closed. I upvoted you :) – farrow90 Dec 02 '24 at 14:49
Your question was closed because you didn't say in your post what you meant by "similar", or what you were trying to achieve, or even give examples of squares you would consider more or less similar, so there was no way to provide you with anything that might substantively help you solve your problem. – MJD Dec 02 '24 at 18:17
@MJD -- that wasn't my question, as for my answer: I've improved it based on your insightful comment -- thanks. – rych Dec 03 '24 at 03:11
@farrow90 Your question is legit: you have up-votes, comments on the question, and an answer! Keep up your research! – rych Dec 03 '24 at 03:15
To the down-voters who run away without comment: could you consider changing your behavior :) – rych Dec 03 '24 at 03:17
@MJD : thank you for the feedback ... I will edit this soon accordingly – farrow90 Dec 03 '24 at 03:46
@rych I was replying to farrow90's comment immedately before, not to you. – MJD Dec 03 '24 at 05:35

How to tell which picture is closest to another picture?

1 Answers1

Linked