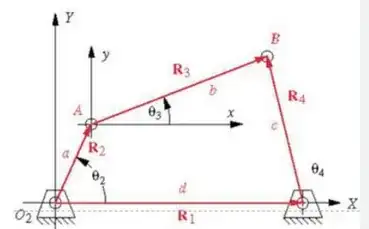
Consider a standard 4-bar mechanism (say a Grashof crank-rocker) with mobility $df = 1$ and its 1D configuration space (c-space) $Q \approx S^1$.
The c-space is essentially $\theta_2$, since, using standard mechanical engineering theory, from this angle, we can deduce $\theta_3$ and $\theta_4$ and uniquely identify the state of the system (up to open and crossed solutions; let us assume for definiteness we always choose the open solution). The velocity vectors to the c-space obviously live in $TQ$.
In this post, the double tangent bundle $TTQ$ is discussed, and, in this post, its horizontal and vertical vector bundles $TTQ = HTQ \oplus VTQ$ are discussed. Also, of course, in standard mechanical engineering theory, there are tangential and normal components of acceleration $\vec{a}_A = \vec{a}^{\bf{T}}_A + \vec{a}^{\bf{N}}_A$.
My question is very simple and very basic (but I don't think my mechanical engineering professor will be able/willing to answer it): can one simply think of $\vec{a}^{\bf{T}}_{\theta_1}$ as, in a way, living in $HTQ$ and $\vec{a}^{\bf{N}}_{\theta_1}$ as living in $VTQ$, so that this provides a natural decomposition of $\vec{a}_{\theta_1}$ in the double tangent bundle of $S^1$?
Also, and this is kind-of a big add-on, if one uses the inertial Riemannian metric (r-metric), as described in https://youtu.be/BjD-pL819LA?si=sKlO6lidDOBXuUYN&t=189 ($M(\theta)$ is the r-metric) and read off the equation of motion (EoM), and if one lifts the r-metric on $TQ$ to $TTQ$ as described in again this post, does one have that $||\vec{a}^{\bf{T}}_A|| = \alpha_1 a$ (the [norm of the?] angular acceleration times the length of link 2, $L_2 = a$) and $||\vec{a}^{\bf{N}}_A|| = \omega^2_1 a$ (the square of the norm of the angular velocity times the length of link 2)?
EDIT: It is noted in this webpage that $M(\theta_1)$ has dimensions of $\text{length}^2 \cdot \text{mass}$, so maybe $||\vec{a}^{\bf{T}}_A|| = \alpha_1 a$ and $||\vec{a}^{\bf{N}}_A|| = \omega^2_1 a$ are too much to ask on that basis alone? Perhaps there's another r-metric on $Q$ that would satisfy the requirements?
Thanks in advance for any assistance you may provide.