Optimal choices in a graph coloring game?

Question

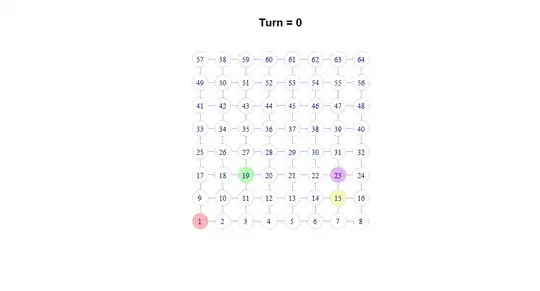
I thought of a game that involves a square lattice graph (e.g. 8x8). At turn=0, we randomly pick 4 nodes ("source nodes") and color each one a separate color :

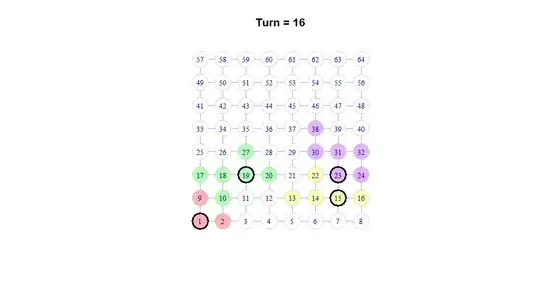
In each turn, a color is randomly selected and has the option to pick any node touching one of its nodes and claim that color - for example (at the end of turn 16, the board looks like this):

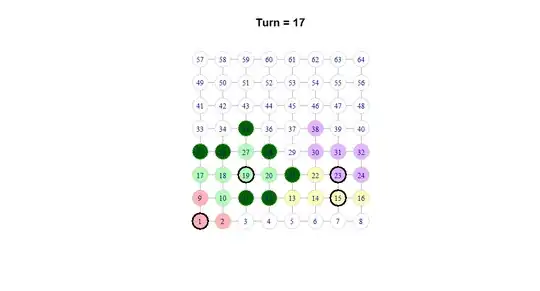
For example, suppose at turn = 17, green is selected. Green has the option of coloring any of the following nodes (in dark green):

The winner is decided at the end of the game with the most popular color.

This leads me to some questions:

• When it comes to the positions of source nodes, are some positions more advantageous than others? (e.g. corners, perimeter, center, etc.)
• At any intermediate point in the game, based on the configuration - is it possible to predict the most likely outcome in which the game will end? e.g. we are currently at turn=16 with purple(5), yellow(4), red(2) and green (5) .... is it possible to know the probability of the final score being: red 60%-yellow 20%-green 10% - purple 10%? Can we do this without the exact positionings - or are the exact positionings needed?
• In general, will the winner of the game win by huge margins? Or will the games be close? E.g. 1st Place Score - 4th Place Score $\leq c$?
• Finally, suppose we are the start of turn 17 and its greens turn. Out of all the possible spots green can currently pick, which one is optimal? Will some of these spots more likely to secure larger regions or interrupt progress of other colors? Or is random choice is the best strategy here?

Can these problems be mathematically answered? Or can they only be simulated?

I am interested in hearing mathematical discussion on this!

PS: I wonder how the above answers would change if the starting graph is a random graph (e.g. erdos remy)

---

Sample R code for problem:

library(igraph)
n <- 8
g <- make_lattice(length=n, dim=2)
layout <- layout_on_grid(g, width=n)
node_colors <- rep("white", vcount(g))
node_colors[c(1,2,9)] <- "#ffb3b3" 
node_colors[c(19,20,10,18,17,27,20)] <- 
node_colors[c(15,16,13,14,22)] <- "#ffffb3" 
node_colors[c(23,24,32,31,30,38)] <- "#e6b3ff"
border_colors <- rep("gray80", vcount(g))
border_colors[c(1,15,23,19)] <- "black"
plot(g, 
     layout=layout,
     vertex.color=node_colors,
     vertex.size=20,
     vertex.label=1:64,
     vertex.label.cex=0.8,
     vertex.frame.color=border_colors,

     vertex.frame.width=ifelse(1:vcount(g) %in% c(1,15,23,19), 3, 1),

     edge.width=1)

Answer 1

I think your game is too complicated to provide mathematical answers to your questions. Instead there can be general strategic suggestions, like those in Reversi or Go, and which were already mentioned in the comments.

Nevertheless we can provide an exhaustive computer analysis for small boards, for instance, $4\times 4$, $4\times 5$ or $5\times 5$, and similarly for small graphs to play. I suggest to deal with the two-color case, because if there are more colors then some of them can cooperate, that makes the strategy analysis hard and I guess in this case we have to look for some equilibrium.

The exhaustive analysis proceeds as follows. We list all feasible positions (I suggest up to symmetries, to save the memory and speed up the analysis). We recursively look for a rating $R(P,c)$ and an optimal node choice $C(P,c)$ for each feasible position $P$ and each selected color $c$ in this position. For this purpose let $\mathcal P(P,c)$ be the set of all positions which can be obtained from $P$ by coloring a feasible chosen node in the color $c$. In the game description is not stated what happens when $\mathcal P(P,c)$ is empty. In this case there is no feasible node choice for the color $c$ anymore, so I guess that then the color $c$ choices are skipped and all remaining choices belong to the other color(s), who color all remaining uncolored nodes. When in the position $P$ there remains only one color with feasible choices, the coloring of the remaining nodes is unique and we shall call the final position the finalization of the position $P$.

So, first we consider all positions where one of two colors cannot choose anymore. For each of these positions we consider its finalization to detect the winner (or the tie). In fact, there can be other positions where there is no way for one of the colors to color at least half of the nodes, so these positions are also winning for the other color. If the position $P$ is winning for the color $c$ then put $R(P,c)=1$ and $R(P,c')=0$, where $c'$ it the feasible color other from $c$. If the position $P$ is a tie then put $R(P,c)=1/2$ for each feasible color $c$.

Now suppose that we are given a position $P$ together with a selected color $c$ such that $R(P,c)$ is undefined yet, but $R(P',c^*)$ is defined for all $P'\in\mathcal P(P,c)$ and all feasible colors $c^*$. Then put $$r(P,c)=\max_{P'\in\mathcal P(P,c)} \frac 12\cdot\left(r(P',c)+1-r(P',c')\right),$$ where $c'$ it the color other from $c$. The optimal choice $C(P,c)$ is that which transforms the position $P$ into $P'$ where the above maximum is attained.