This summer, I had posted some questions on better understanding Polya's Urn (https://en.wikipedia.org/wiki/P%C3%B3lya_urn_model) problem in probability theory:
The basic Polya Urn problem is as follows:
- Start with an urn containing $r_0$ red balls and $b_0$ blue balls. At each step $n \geq 1$:
- Draw a ball uniformly at random
- Return the ball to the urn
- Add one more ball of the same color
If $(R_n, B_n)$ be the number of red and blue balls after $n$ steps. Then:
$$P(R_{n+1} = R_n + 1 | R_n, B_n) = \frac{R_n}{R_n + B_n}$$ $$P(B_{n+1} = B_n + 1 | R_n, B_n) = \frac{B_n}{R_n + B_n}$$
Supposedly, if we start with the same number of red and blue balls, the distribution of the long term ratio follow a Uniform Probability Distribution. If we start with different numbers of red and blue balls, the distribution of the long term ratio follow a Beta Probability Distribution.
I am interested in knowing what happens if there are multiple colors. For example:
Start with an urn containing $c_i^{(0)}$ balls of color $i$ for $i = > 1,\ldots,n$ colors. At each step $k \geq 1$:
- Draw a ball uniformly at random
- Return the ball to the urn
- Add one more ball of the same color
Mathematically, let $c_i^{(k)}$ be the number of balls of color $i$ after $k$ steps. Then:
$$P(c_i^{(k+1)} = c_i^{(k)} + 1 | c_1^{(k)},\ldots,c_n^{(k)}) = > \frac{c_i^{(k)}}{\sum_{j=1}^n c_j^{(k)}}$$
I saw some questions posted on this topic (e.g. Establishing bounds on Pólya's Urn for three colors and two draws after $N$ draws, Generalized Polya's Urn, Probability... Urn problem with multiple colors, multiple draws and a given condition), but I was looking for some more conclusive results on this.
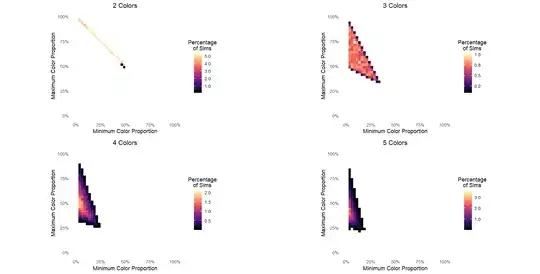
For example, if there are more than 2 colors, it seems to hard define a ratio of colors. In this case, I thought of defining the distribution of the most popular color vs the least popular color after a certain number of simulations. I tried to do this in R (starting with an equal number of balls):
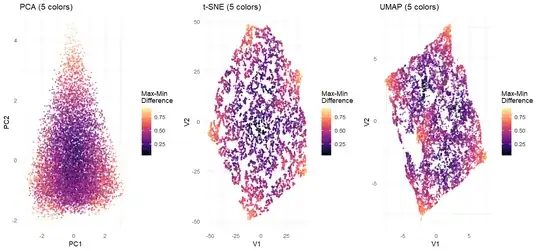
While a bit unorthodox, I then tried to use some Machine Learning based dimensionality reduction techniques to visualize the results from a different perspective (this uses the actual final proportional of all colors in each simulations):
In general, are there any mathematical results on this problem? E.g. the limiting distribution for $n$ colors is Dirichlet or Multinomial?