Issues when calculating the Cauchy principal value of $\int _0^1\frac{\ln ^2\left(x\right)}{1-2x}\:\mathrm{d}x$

Question

The following problem was proposed online: $$\operatorname{P.V.}\int _0^1\frac{\ln ^2\left(x\right)}{1-2x}\:\mathrm{d}x=i\pi \ln ^2\left(2\right)+\operatorname{Li}_3\left(2\right)$$ $\displaystyle\operatorname{P.V.}\int _a^bf\left(x\right)\:\mathrm{d}x$ is the Cauchy principal value for that integral and $\operatorname{Li}_3\left(z\right)$ is the trilogarithm.

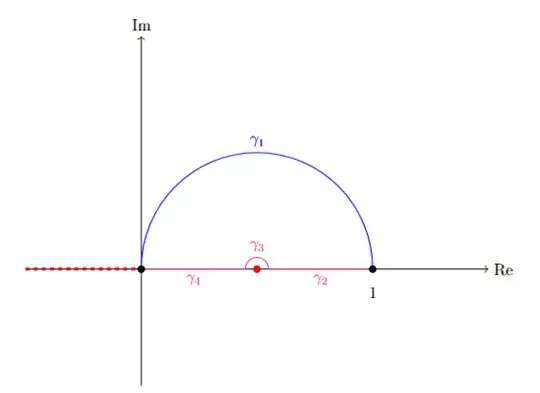
My attempt is the following: $$\operatorname{P.V.}\int _0^1\frac{\ln ^2\left(x\right)}{1-2x}\:\mathrm{d}x=\lim _{\epsilon \to 0^+}\left(\int _0^{\frac{1}{2}-\epsilon }\frac{\ln ^2\left(x\right)}{1-2x}\:\mathrm{d}x+\int _{\frac{1}{2}+\epsilon }^1\frac{\ln ^2\left(x\right)}{1-2x}\:\mathrm{d}x\right)$$ and $$\int \frac{\ln ^2\left(x\right)}{1-2x}\:\mathrm{d}x=-\frac{1}{2}\ln ^2\left(x\right)\ln \left(1-2x\right)-\ln \left(x\right)\operatorname{Li}_2\left(2x\right)+\operatorname{Li}_3\left(2x\right)+C$$ so $$\operatorname{P.V.}\int _0^1\frac{\ln ^2\left(x\right)}{1-2x}\:\mathrm{d}x$$ $$=\lim _{\epsilon \to 0^+}\left(-\frac{1}{2}\ln ^2\left(\frac{1}{2}-\epsilon \right)\ln \left(2\epsilon \right)-\ln \left(\frac{1}{2}-\epsilon \right)\operatorname{Li}_2\left(1-2\epsilon \right)+\operatorname{Li}_3\left(1-2\epsilon \right)+\operatorname{Li}_3\left(2\right)+\frac{1}{2}\ln ^2\left(\frac{1}{2}+\epsilon \right)\ln \left(-2\epsilon \right)+\ln \left(\frac{1}{2}+\epsilon \right)\operatorname{Li}_2\left(1+2\epsilon \right)-\operatorname{Li}_3\left(1+2\epsilon \right)\right)$$ $$=\frac{i\pi }{2}\ln ^2\left(2\right)+\operatorname{Li}_3\left(2\right)$$ According to the problem proposer this result is "wrong" as they have utilized software tools to verify it. I tried calculating the principal value with Mathematica as well and it gave me the same "wrong" answer.

Am I making a mistake? Is there something I am missing?

Thank you.

---

Edit. We have that $$\int _0^{\infty }\frac{\ln ^2\left(\frac{1+ix}{1+x^2}\right)}{x\left(1+x^2\right)}\:\mathrm{d}x=\int _0^1\frac{\ln ^2\left(x\right)}{1-x}\:\mathrm{d}x-\operatorname{P.V.}\int _0^1\frac{\ln ^2\left(x\right)}{1-2x}\:\mathrm{d}x$$ Numerically we have that $$\int _0^{\infty }\frac{\ln ^2\left(\frac{1+ix}{1+x^2}\right)}{x\left(1+x^2\right)}\:\mathrm{d}x\approx-0.357958-0.754694 i$$ Using the (wrong) result I obtained would yield $$\int _0^{\infty }\frac{\ln ^2\left(\frac{1+ix}{1+x^2}\right)}{x\left(1+x^2\right)}\:\mathrm{d}x=2\zeta \left(3\right)-\frac{i\pi }{2}\ln ^2\left(2\right)-\operatorname{Li}_3\left(2\right)$$ $$\approx-0.357958$$ If instead, the proposed result is used $$\int _0^{\infty }\frac{\ln ^2\left(\frac{1+ix}{1+x^2}\right)}{x\left(1+x^2\right)}\:\mathrm{d}x=2\zeta \left(3\right)-i\pi \ln ^2\left(2\right)-\operatorname{Li}_3\left(2\right)$$ $$\approx-0.357958-0.754694 i$$ Conclusion. This edit suggests that the integral in question is supposed to yield a complex number, not a real one.

Answer 1

$\newcommand{\bbx}[1]{\,\bbox[15px,border:1px groove navy]{\displaystyle{#1}}\,} \newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack} \newcommand{\dd}{\mathrm{d}} \newcommand{\ds}[1]{{\displaystyle #1}} \newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,} \newcommand{\ic}{\mathrm{i}} \newcommand{\iverson}[1]{\left[\left[\,{#1}\,\right]\right]} \newcommand{\on}[1]{\operatorname{#1}} \newcommand{\pars}[1]{\left(\,{#1}\,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,} \newcommand{\sr}[2]{\,\,\,\stackrel{{#1}}{{#2}}\,\,\,} \newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$ \begin{align} & \color{#44f}{\operatorname{P.V.}\int_{0}^{1} {\ln^{2}\pars{x} \over 1 - 2x}\dd x} \sr{2x\ \mapsto\ x}{=} {1 \over 2}\operatorname{P.V.}\int_{0}^{2} {\ln^{2}\pars{x/2} \over 1 - x}\dd x \\[5mm] = & \ {1 \over 2}\lim_{\epsilon\ \to\ 0^{+}}\,\bracks{% \int_{0}^{1 - \epsilon}\, {\ln^{2}\pars{x/2} \over 1 - x}\dd x + \int_{1 + \epsilon}^{2}\,\, {\ln^{2}\pars{x/2} \over 1 - x}\dd x} \\[5mm] = & \ {1 \over 2}\!\lim_{\epsilon\ \to\ 0^{+}}\,\bracks{\!% \int_{0}^{1 - \epsilon} {\ln^{2}\pars{x/2} \over 1 - x}\dd x - \int_{1/2}^{1/\pars{1 + \epsilon}}\! {\ln^{2}\pars{2x} \over x\pars{1 - x}}\dd x\!\!} \label{1}\tag{1} \\[5mm] = & \ {1 \over 2}\lim_{\epsilon\ \to\ 0^{+}}\,\bracks{% \int_{0}^{1 - \epsilon}\, {\ln^{2}\pars{x/2} \over 1 - x}\dd x - \int_{1/2}^{1/\pars{1 + \epsilon}}\,\, {\ln^{2}\pars{2x} \over 1 - x}\dd x}\label{2}\tag{2} \\[2mm] & \phantom{{1 \over 2}\lim_{\epsilon\ \to\ 0^{+}}\,\bracks{}}-\ \underbrace{{1 \over 2}\int_{1/2}^{1}{\ln^{2}\pars{2x} \over x}\dd x} _{\ds{\ln^{3}\pars{2}/6}} \end{align} In (\ref{1}), I made the change $\ds{x\ \mapsto\ 1/x}$ to avoid $\ds{\ln}$'s with negative argument.

It's straightforward to show that, by integrating by parts successively ( see (\ref{2}) ), $$ \left\{\begin{array}{l} \ds{\int{\ln^{2}\pars{ax} \over 1 - x}\dd x} \\ \ds{= -\ln\pars{1 - x}\ln^{2}\pars{ax} - 2\ln\pars{ax}\on{Li}_{2}\pars{x} + 2\on{Li}_{3}\pars{x}} \\ \ds{\equiv \varphi\pars{a,x}} \end{array}\right. $$ Therefore $\ds{\pars{~\mbox{with}\ \lim_{x\ \to\ 0^{+}}\,\,\,\varphi\pars{a,x} = 0}}$ -, \begin{align} & \color{#44f}{\operatorname{P.V.}\int_{0}^{1} {\ln^{2}\pars{x} \over 1 - 2x}\dd x} \\[3mm] = & \ {1 \over 2}\lim_{\epsilon\ \to\ 0^{+}}\,\,\braces{% \varphi\pars{{1 \over 2},1 - \epsilon} - \bracks{\rule{0pt}{5mm}\varphi\pars{2,{1 \over 1 + \epsilon}} - \varphi\pars{2,{1 \over 2}}}} \\ & \ -{\ln^{3}\pars{2} \over 6} \\[5mm] = & \ {1 \over 2}\varphi\pars{2,{1 \over 2}} + \overbrace{{1 \over 2}\lim_{\epsilon\ \to\ 0^{+}}\,\,\bracks{% \varphi\pars{{1 \over 2},1 - \epsilon} - \varphi\pars{2,{1 \over 1 + \epsilon}}}}^{\ds{\pi^{2}\ln\pars{2}/3}} \\[2mm] & - {\ln^{3}\pars{2} \over 6} \end{align} With $$ {1 \over 2}\varphi\pars{2,{1 \over 2}} = {7\zeta\pars{3} \over 8} + {\ln^{3}\pars{2} \over 6} - {\pi^{2}\ln\pars{2} \over 12} $$ the final result becomes $$ \color{#44f}{\operatorname{P.V.}\int_{0}^{1} {\ln^{2}\pars{x} \over 1 - 2x}\dd x} = \bbx{\color{#44f}{{7\zeta\pars{3} \over 8} + {\pi^{2}\ln\pars{2} \over 4}}} \approx 2.7621 $$

Answer 2

The question this answer is focused on is:

"Am I making a mistake? Is there something I am missing?"

We already have answers, that recompute the integral and find the one or the other shape. Here is a way to validate the answer for the relation: $$ J:= \operatorname{PV} \int_0^1 \frac{\ln^2 x}{1-2x}\;dx =\frac i2\pi \ln^2 2+ \operatorname{Li}_3\left(2\right) \ . $$ Yes, it is correct, we find below alternative forms of the same number using the functional relations of the trilogarithm, and check numerically to a high precision. Because the claimed alternative answer differs by an imaginary complex number, this last answer is wrong.

---

• One objection would be the fact that the number "looks like a complex number" (and does not "look like a real number"). So let us make it look like and be a real number. The trilogarithm satisfies some functional equations, and i am using wolfram relations for the trilogarithm to obtain closer information on its value in two. We let $z$ be $z=-2$ in the second identity listed under $(1)$ in this link, and obtain: $$ \tag{$1^*$} \operatorname{Li}_3\left(2\right) - \operatorname{Li}_3\left(\frac 12\right) = -\frac 16\ln^3(-2) -\frac 16\pi^2\ln(-2) \\ = -\frac 16(\ln^3 2 -2\pi^2\ln 2)-\frac i2\pi\ln^2 2\ . $$ This gives a formula for the wanted PV-integral: $$ \bbox[yellow]{\qquad J = \operatorname{Li}_3\left(\frac 12\right) -\frac 16(\ln^3 2 -2\pi^2\ln 2) \ ,\qquad} $$ which can be easier verified numerically.

---

• Let us use pari/gp to get the numerical value of the integral. For this, we need an expresion "without the $P.V.$ ingredient". So we use the substitution $y=x-\frac 12$, obtain an integral w.r.t. $dy$ from $-\frac 12$ to $\frac 12$, split it as $\int_{-1/2}^{0_-} + \int_{0_+}^{1/2}$ (with corresponding values $0_-$ and $0^+$, so that their sum is a pure zero, then pass to the limit, Cauchy principal value), and the first piece gets a substitution $y\to-y$ to have one integral on $[0,\ 1/2]$, which is now convergent. The expression for it is $$ J = -\frac 12\int_0^{1/2} \log\Big(\frac{1/2+y}{1/2-y}\Big) \log\Big((1/2+y)(1/2-y)\Big) \; \frac {dy}y\ , $$and pari/gp gives the approximate value

? \p 80
   realprecision = 96 significant digits (80 digits displayed)
? -1/2 * intnum(y=0, 1/2, log((1/2+y)/(1/2-y)) * log((1/2+y)*(1/2-y)) / y)
%32 = 2.7620719062289241359366406798110427597443077678449149003992705730533877397937161
? polylog(3, 1/2) - 1/6(log(2)^2 - 2Pi^2)*log(2)
%33 = 2.7620719062289241359366406798110427597443077678449149003992705730533877397937161

For the expression of the integral algebrically obtained in terms of the trilogarithm of $1/2$, $\pi$, and $\ln 2$, we have numerically the same value...

---

• We can stop here, but an alternative view may be also interesting. We let $z$ be $z=2$ in the third identity listed under $(1)$ the same wolfram link, and obtain: $$ \tag{$1^{**}$} \operatorname{Li}_3(2) + \underbrace{\operatorname{Li}_3(-1)}_{-\frac 34\zeta(3)} + \operatorname{Li}_3\left(\frac 12\right) = \zeta(3)+\frac 16\ln^3 2+\frac 16\pi^2\ln 2 -\frac 12\ln^2 2\ln(-1)\ . $$ This gives a formula for the wanted PV-integral in terms of $\zeta(3)$, $\pi$, and $\ln 2$ (after using the known relation $(1^*)$ for the difference between the trilogarithm values in $2$ and $1/2$, and we add it to $(1^**)$ to isolate a formula for $\operatorname{Li}_3(2)$: $$ \bbox[lightgreen]{\qquad \begin{aligned} \operatorname{Li}_3(2) &= \frac 78\zeta(3) +\frac 14\pi^2\ln 2 -\frac i2\pi\ln^2 2\ , \\[2mm] J &=\frac 78\zeta(3)+\frac 14\pi^2\ln 2\ . \end{aligned} \qquad} $$

---

• Which can be again verified numerically:

? J = -1/2 * intnum(y=0, 1/2, log((1/2+y)/(1/2-y)) * log((1/2+y)*(1/2-y)) / y)
%47 = 2.7620719062289241359366406798110427597443077678449149003992705730533877397937161
? 7/8*zeta(3) +  Pi^2/4*log(2)
%48 = 2.7620719062289241359366406798110427597443077678449149003992705730533877397937161

---

Conclusion: Starting from the given claimed answer, from the claim value of $J$, it was validated by reshaping it so that only a real number survives, there is no imaginary part (from the trilogarithm computed in $2$) any more, and numerically the values are matching.

Answer 3

Using Mathematica with the same steps $$I_1=\int_0^{\frac 12-\epsilon} \frac{\log ^2(x)}{1-2 x}\,dx$$ $$I_1=\text{Li}_3(1-2 \epsilon )-\frac{1}{2} \log \left(\frac{1}{2}-\epsilon \right) \left(2 \text{Li}_2(1-2 \epsilon )+\log \left(\frac{1}{2}-\epsilon \right) \log (2 \epsilon )\right)$$

$$I_2=\int_{\frac 12+\epsilon}^1 \frac{\log ^2(x)}{1-2 x}\,dx$$ $$I_2=-\text{Li}_3(2 \epsilon +1)+\text{Li}_2(2 \epsilon +1) \log \left(\epsilon +\frac{1}{2}\right)+\frac{7 \zeta (3)}{8}+\frac{1}{2} \log (2 \epsilon ) \log ^2\left(\frac{2}{2 \epsilon +1}\right)+$$ $$\frac{1}{2} i \pi \log ^2\left(\frac{2}{2 \epsilon +1}\right)-\frac{1}{2} i \pi \log ^2(2)+\frac{1}{8} \pi ^2 \log (4)$$

Expanding as a series $$I_1+I_2=\frac{7 \zeta (3)+\pi ^2 \log (4)}{8} -4 \log (2)\,\epsilon -\frac{8(3+2 \log(2))}{9} \,\epsilon ^3+O\left(\epsilon ^5\right)$$

which is the result given by Mathematica using the PrincipalValue->Trueoption.

You can check all the results using $\epsilon=10^{-3}$.

Notice that $$\text{Li}_3(2)+\frac{1}{2} i \pi \log ^2(2)=\frac{7 \zeta (3)+\pi ^2 \log (4)}{8} $$

I do not see anything wrong in the result.

Answer 4

Start with $$I = \operatorname{P.V.}\int _0^1\frac{\ln ^2\left(x\right)}{1-2x}\:\mathrm{d}x.$$

Make the substitution $u=2x$,

$$I = \operatorname{P.V.}\int _0^2\frac{\ln ^2\left(\frac{u}{2}\right)}{2(1-u)}\:\mathrm{d}u$$ But we can expand the log as $\ln ^2\left(\frac{u}{2}\right) = \ln ^2\left(u\right)-2\ln(2)\ln(u)+\ln ^2\left(2\right)$: $$I= \int _0^2\frac{\ln ^2\left(u\right)-2\ln(2)\ln(u)}{2(1-u)}\:\mathrm{d}u+\operatorname{P.V.}\int _0^2\frac{\ln ^2\left(2\right)}{2(1-u)}\:\mathrm{d}u.$$ In the first integral, the integrand is smooth, meaning the principal value is just the integral itself. The final integral is easily found to be zero.

This gives

$$I=i\frac{\pi}{2} \ln ^2\left(2\right)+\operatorname{Li}_3\left(2\right)\approx 2.762.$$

Answer 5

I'd like to address the edits here. The resolution is subtle, and interesting, enough that I think it deserves to be highlighted in a separate answer.

As I've stated elsewhere, the values of $\int _0^1\frac{\ln ^2\left(x\right)}{1-x}\:\mathrm{d}x-\operatorname{P.V.}\int _0^1\frac{\ln ^2\left(x\right)}{1-2x}\:\mathrm{d}x$ must be real because the integrands are real. But, I also replicate your numerical results for that the integral, $$I=\int _0^{\infty }\frac{\ln ^2\left(\frac{1+ix}{1+x^2}\right)}{x\left(1+x^2\right)}\:\mathrm{d}x,$$ has a nontrivial imaginary part. So, the problem must be in the transformation from the latter to the former. Let's examine it more closely. $I$ can be written as a contour integral, $$I=\oint_{\xi} F(z)\:\mathrm{d}z,$$ where, $$F(z)=\frac{\ln ^2\left(\frac{1+iz}{1+z^2}\right)}{z\left(1+z^2\right)},$$ with $\ln$ being on the principal branch, and $\xi$ is the contour along the positive real line from $0$ to $\infty$.

Let $w(z)=i\frac{1-z}{z}$ so that $w^{-1}(z)=\frac{1+iz}{1+z^2}=\frac{i}{z+i}$. By the contour integral chain rule, $$I= \oint_{\gamma_1}F(w(z))w'(z)\:\mathrm{d}z=\oint_{\gamma_1}\ln ^2\left(z\right)\left[\frac{1}{z-1}-\frac{1}{2z-1}\right]\:\mathrm{d}z.$$ Crucially, here $\gamma_1$ is the image of $\xi$ under $w^{-1}$. Via the theory of mobius functions, we can see that $\gamma_1$ is the semicircular contour running from $z=1$ to $z=0$ shown in blue below.

Here we see a subtlety of substitution in contour integrals not present for real integrals. Straight line contours usually don't transform into straight lines after a change of variables. You cannot always simply integrate along a straight line between the endpoints like you do with real integrals. In this case, this was obscured because the start and endpoints were on the real line, making it seem like the result was a real integral. But, to equal the original integral $J$, you must take the integral along $\gamma_1$, or something homotopically equivalent.

This also explains appearance of a singularity after substitution, which shouldn't happen if there was no singularity before and the substitution was smooth. This is resolved because there is no singularity on $\gamma_1$. It's only if you try to take the contour directly from $1$ to $0$ that you run into a singularity at $w^{-1}(i)=\frac{1}{2}$, which corresponds to the singularity at $i$ in the original integrand.

By Cauchy's theorem, we can instead integrate along the magenta contour $\gamma_2+\gamma_3+\gamma_4$ shown below, $$J = \oint_{\gamma_2}\ln ^2\left(z\right)\left[\frac{1}{z-1}-\frac{1}{2z-1}\right]\:\mathrm{d}z+\oint_{\gamma_4}\ln ^2\left(z\right)\left[\frac{1}{z-1}-\frac{1}{2z-1}\right]\:\mathrm{d}z$$$$+\oint_{\gamma_3}\ln ^2\left(z\right)\left[\frac{1}{z-1}-\frac{1}{2z-1}\right]\:\mathrm{d}z.$$

In the limit of the radius of $\gamma_3$ approaching zero, the integrals along $\gamma_2$ and $\gamma_4$ become the integrals,

$$\oint_{\gamma_2+\gamma_4}\ln ^2\left(z\right)\left[\frac{1}{z-1}-\frac{1}{2z-1}\right]\:\mathrm{d}z=\int _0^1\frac{\ln ^2\left(x\right)}{1-x}\:\mathrm{d}x-\operatorname{P.V.}\int _0^1\frac{\ln ^2\left(x\right)}{1-2x}\:\mathrm{d}x$$$$=2\zeta \left(3\right)-i\frac{\pi}{2} \ln ^2\left(2\right)-\operatorname{Li}_3\left(2\right).$$

But, in the limit of zero radius, the integral around $\gamma_3$ is nonzero. By a standard complex analysis result, it is $$\oint_{\gamma_3}\ln ^2\left(z\right)\left[\frac{1}{z-1}-\frac{1}{2z-1}\right]\:\mathrm{d}z=\pi i\mathrm{Res}(\ln ^2\left(z\right)\left[\frac{1}{z-1}-\frac{1}{2z-1}\right],\frac{1}{2})$$$$=-i\frac{\pi }{2}\ln ^2\left(2\right). $$ This gives a value of $I$ that matches the numerical result: $$I=2\zeta \left(3\right)-i\pi \ln ^2\left(2\right)-\operatorname{Li}_3\left(2\right).$$

Answer 6

Let's start with the following:

$$I(a)=\operatorname{P.V.}\int_{0}^{1}\frac{x^a}{1-2x}dx$$

From here we get back to the original integral by differentiating twice with respect to $a$ and then taking $a=0$

Change of variable $t=2x$:

$$I(a)=\operatorname{P.V.}\frac{1}{2^{a+1}}\int_{0}^{2}\frac{t^a}{1-t}dt=$$

$$=\frac{1}{2^{a+1}}\displaystyle \lim_{\alpha \to 0} \left [\int_{0}^{1-\alpha}\frac{t^a}{1-t}dt + \int_{1+\alpha}^{2}\frac{t^a}{1-t}dt\right ]=$$

$$=\frac{1}{2^{a+1}}\int_{0}^{1}\frac{(1-t)^a-(1+t)^a}{t}dt$$

Let's formulate an intermediate result:

$$\operatorname{P.V.}\int_{0}^{1}\frac{x^a}{1-2x}dx=\frac{1}{2^{a+1}}\int_{0}^{1}\frac{(1-x)^a-(1+x)^a}{x}dx$$

To get the result we are looking for we differentiate this result twice with respect to $a$ and take $a=0$. Then we need to calculate four logarithmic integrals:

$$\int_{0}^{1}\frac{\ln^n(1\pm x)}{x}dx;n=1,2 $$

These integrals appear in closed form

As a result, we get what we are looking for:

$$\operatorname{P.V.}\int _0^1\frac{\ln ^2\left(x\right)}{1-2x}\:\mathrm{d}x=\frac{\pi^2}{4}\ln 2 + \frac{7}{8}\zeta \left(3\right)=2.762...$$

Answer 7

General Clarification

(Not an Answer)

---

To calculate the integral $\displaystyle\int\limits_{o}^{\infty}\frac{\log^2{\left(\frac{1+ix}{1+x^2}\right)}}{1+x^2}\frac{dx}{x}\,$ by the substitution $\displaystyle\left\{x=\frac{t-1}{i\,t} \Rightarrow t=\frac{1+ix}{1+x^2}\right\}\,$,
We construct a contour $\left(\text{i.e.}\,\, {\int\limits_{\small0}^{i}{\small+}\int\limits_{i}^{\small1}}\right)$ avoid the singularity at $\displaystyle\left\{x=i \Rightarrow t={\small\frac12}\right\}\,$: $$ \int\limits_{o}^{\infty}\frac{\log^2{\left(\frac{1+ix}{1+x^2}\right)}}{1+x^2}\frac{dx}{x} = \underbrace{\int\limits_{0}^{1}\frac{{\small-}\log^2t}{t-1}\,dt}_{\large 2\zeta(3)} \,\,+\,\, \color{blue}{\underbrace{{\int\limits_{0}^{i}+\int\limits_{i}^{1}}\, {\frac{{\small-\frac12}\log^2t}{t-{\small\frac12}}\,dt}}_{\large {i\pi\log^22}\,+\,\text{Li}_3(2)}} $$

---

By Sokhotski–Plemelj theorem: $$ \lim_{\epsilon\to0^+}\int\limits_{a}^{b}\frac{f(x)}{x-x_{_0}{\small\pm}i\epsilon}\,dx = {\small\mp}i\pi f{(x_{_0})} + {\text{PV}\int\limits_{a}^{b}}\frac{f(x)}{x-x_{_0}}\,dx $$ Thus, the Cauchy Principal Value of the integral $\displaystyle\,\, {\text{PV}\int\limits_{0}^{1}}\frac{{\small-\frac12}\log^2t}{t-{\small\frac12}}\,dt$ $\,\color{red}{\text{over the real line}}\,$ is defined to be equal to: $$ {\text{PV}\int\limits_{0}^{1}}\frac{{\small-\frac12}\log^2t}{t-{\small\frac12}}\,dt = \color{red}{\underbrace{{\small\mp}i\frac{\pi}{2}\log^2\left(\frac12\right)}_{\large i\frac{\pi}{2}\log^22}\,+\, \underbrace{\lim_{\epsilon\to0^+}\int_{0}^{1}\frac{{\small-\frac12}\log^2t}{x-{\small\frac12}{\small\pm}i\epsilon}\,dx}_{\large \text{Li}_3(2)}} $$

---

So the statement: $$ \int\limits_{o}^{\infty}\frac{\log^2{\left(\frac{1+ix}{1+x^2}\right)}}{1+x^2}\frac{dx}{x} = \int\limits_{0}^{1}\frac{\log^2t}{1-t}\,dt - \text{PV}\int\limits_{0}^{1}\frac{\log^2t}{1-2t}\,dt $$ $\,\color{red}{\text{Is miss leading}}\,$, because $\displaystyle\left\{\text{PV}\right\}$ usually refer to Principal Value over the real line,
Not only because it matchs the calculations, but also because it obeys the theorem.

$$ \begin{align} \color{blue}{\int_{{\large C}_{_{[0,1]}}}{\frac{\log^2x}{1-2x}\,dx}} &\,\,\, \color{blue}{=i\pi\log^22 + \text{Li}_3(2)} \\[2mm] \color{red}{\text{PV}\int\limits_{0}^{1}\frac{\log^2x}{1-2x}\,dx} &\,\,\, \color{red}{=i\frac{\pi}{2}\log^22 + \text{Li}_3(2)} \end{align} $$

---

If otherwise we define: $$ \begin{align} f(x) =& \int\frac{\log^2{\left(\frac{1+ix}{1+x^2}\right)}}{1+x^2}\frac{dx}{x} \\[2mm] \implies &\int\limits_{o}^{\infty}\frac{\log^2{\left(\frac{1+ix}{1+x^2}\right)}}{1+x^2}\frac{dx}{x} = \left[\,f(x)\,\right]_{\small0}^{\small\infty} = 2\zeta(3)-i\pi\log^22-\text{Li}_3(2) \end{align} $$ Then how to explain: $$ \begin{align} \int\limits_{o}^{\infty}\frac{\log^2{\left(\frac{1+ix}{1+x^2}\right)}}{1+x^2}\frac{dx}{x} &= \int\limits_{o}^{\color{red}{i-\epsilon}}\frac{\log^2{\left(\frac{1+ix}{1+x^2}\right)}}{1+x^2}\frac{dx}{x} + \int\limits_{\color{red}{i+\epsilon}}^{\infty}\frac{\log^2{\left(\frac{1+ix}{1+x^2}\right)}}{1+x^2}\frac{dx}{x} \\[2mm] &= {\underbrace{\left[\,\lim_{x\to\infty}f(x)\right]-\left[\,\lim_{x\to0}f(x)\right]}_{\large 2\zeta(3)-i\pi\log^22-\text{Li}_3(2)}} + \color{red}{\underbrace{\lim_{\epsilon\to0^{\small+}}\left[f(i{\small-}\epsilon)-f(i{\small+}\epsilon)\right]}_{\large \frac52i\pi\log^22\,\ne\,0\,\text{??}}} \end{align} $$