How to calculate the distance between a spherical coordinate and a longitude line

Question

How to Calculate Great-Circle Distance to a Longitude Line?

In a spherical coordinate system (e.g., Earth's latitude and longitude):

• I have a point $(\phi, \lambda)$ (latitude and longitude, respectively).
• I also have a fixed longitude line (defined by a single $\lambda_0$).

I want to calculate the great-circle distance from the point to the longitude line. Specifically, this is the distance along the surface of the sphere to the closest point on the longitude line.

My Thoughts

• Initially, I thought this is the same as the distance between $(\phi, \lambda)$ and $(\phi, \lambda_0)$, but I realized this is incorrect except at the equator.
• I believe the correct answer involves finding the great-circle path that is perpendicular to the longitude line, but I am unsure how to compute this.

Question

How can I calculate this great-circle distance? What is the formula or method?

Answer 1

---Edited 18 Nov 2024: The previous calculation of $B$, the bearing to the point of intersection with the specified line of longitude, was incomplete. This has now been corrected.---

The natural tool for such problems is Spherical Trigonometry.

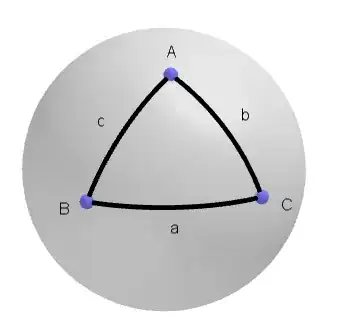
The figure above depicts a typical spherical triangle. The sides of the triangle are arcs of great circles. A great circle is the intersection of the sphere with a plane that passes through the center of the sphere. Unlike plane triangles, the sides of the triangle ($a, b$ and $c$) are measured in radians or degrees, not linear units. I'll assume we are using radians throughout.

For your question, let's suppose vertex $A$ is at the North Pole and your location is vertex $B$ with co-latitude $\phi_0$ and longitude $\lambda_0$. The co-latitude is zero at the North Pole and $\pi/2$ at the equator, unlike geographical latitude which is $\pi/2$ at the North Pole and zero at the equator. Further suppose that $b$ is the line of longitude you want to reach with longitude $\lambda_1$, and $C$ is a right angle. We want to find $a$, the least spherical distance from your location to the designated line of longitude.

To this end, we may apply the Spherical Law of Sines in the form $$\frac{\sin A}{\sin a} = \frac{\sin C}{\sin c}$$ Here $A = \lambda_1 - \lambda_0$, $C= \pi/2$, and $c = \phi_0$, so $$\frac{\sin(\lambda_1 - \lambda_0)}{\sin a} = \frac{\sin{\pi/2}}{\sin \phi_0}$$ which is easily solved for $\sin a$. Taking the inverse sine then yields $a$. If you want the terrestrial distance, find $a$ in radians and multiply $a$ by the radius of the earth.

A natural question is what is the measure of $B$, the bearing from your location to $C$? This is a two-step process. First, for a spherical triangle in which $C$ is a right triangle, the following identity holds: $$\cos c = \cos a \cos b$$ (This is rule R1 in the Wikipedia article on Spherical Trigonometry.) Since we know $a$ and $c$, we can now solve for $\cos b$ and calculate $b$. Second, we may apply the Spherical Law of Cosines in the form $$\cos b = \cos a \cos c + \sin a \sin c \cos B$$ Since we now know $a, b$ and $c$, this equation may be easily solved for $\cos B$.