1

Recently I came across an exercise where we were asked to prove that the family of 1-planar graphs is not minor-closed. In this article they give an example (figure 2) and say that after contracting edge $(2,4)$, the obtained graph is not planar.

image taken from the article

Now, when I try, I obviously fail to draw it in a 1-planar way, but the futility of my attempts does not really mean anything. My question is: how can one see in general that a given graph is not 1-planar, and how can we see it in this specific case?

Thanks in advance!

hajduzs
  • 13
  • The idea is from @MishaLavrov (posted as a comment on my deleted wrong answer), so I will let it eventually post it as an answer. It is known that 1-planar graphs have a maximum of $4n-8$ edges. Such a graph is called optimal 1-planar graph and is Eulerian (see https://en.wikipedia.org/wiki/1-planar_graph#Edge_density). After contracting $(2, 4)$, the graph has $4n-8$ edges but is not Eulerian. – caduk Nov 13 '24 at 10:06
  • @caduk Thanks, this also helps making thing more clear :) – hajduzs Nov 13 '24 at 10:18

2 Answers2

2

I was going to try to give some intuition on why the graph after contracting $(2,4)$ is not $1$-planar, by trying to argue roughly that the two high degree vertices must be in distinct faces of the cycle you get from the other vertices except the contracted vertex, and so on. But $1$-planar graphs are more annoying to argue about that planar graphs, so instead I give an alternate argument for why $1$-planar graphs are not closed under minors.

Using Euler's formula, one can show (see this answer) that a $1$-planar graph on $n$ vertices has has at most $4n-8$ edges, so for instance, $K_7$ is not $1$-planar. So we know not all graphs are $1$-planar. Let $H$ be such a graph, and let $H$ be embedded in the plane. Since $H$ is not $1$-planar, some edges have at least two crossings. For each such edge, place a degree two vertex between every consecutive pair of crossing points. The newly obtained graph is $1$-planar, and contains $H$ as a (topological) minor, as desired.

Mathieu Rundström
  • 3,647
1

We need two properties of $1$-planar graphs:

  1. An $n$-vertex planar graph can have at most $4n-8$ edges.
  2. If the $n$-vertex planar graph is optimal, and has exactly $4n-8$ edges, then all vertex degrees are even.

The first property is addressed in this question. For the second, we argue that when we hit the limit of $4n-8$ edges, it means that the $1$-planar drawing divides the plane into exclusively triangular regions, and each corner of each region includes two of the vertices and one crossing between the edges.

Therefore for any two consecutive edges coming out of a vertex, exactly one must have a crossing. In other words, the crossing and non-crossing edges out of a vertex must alternate! This forces the degree to be even, because there is an equal number of each type of edge coming out of each vertex.

With this in mind, how do we prove that the graph in the question stops being $1$-planar when we contract edge $24$?

Well, the original graph has $10$ vertices and $32 = 4\cdot 10 - 8$ edges, and the contracted graph has $9$ vertices and $28 = 4\cdot 9 - 8$ edges. So both of them, if they are $1$-planar, must be optimal $1$-planar graphs. The original graph, shown below, is actually a good illustration of everything I've said about the properties of such graphs:

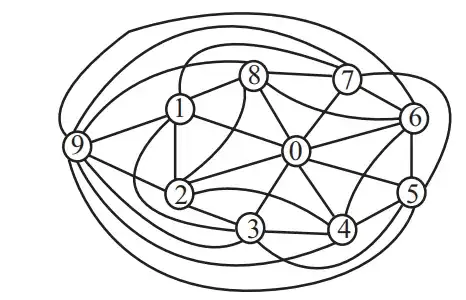
The 1-planar graph in the question

However, in the contracted graph, not all vertex degrees are even: any vertex that was adjacent to both $2$ and $4$ (such as for example vertex $0$) now has odd degree, and in fact the vertex created by contraction also has odd degree. So it does not satisfy the properties of an optimal $1$-planar graph - and therefore, it cannot be $1$-planar.

Misha Lavrov
  • 159,700