2

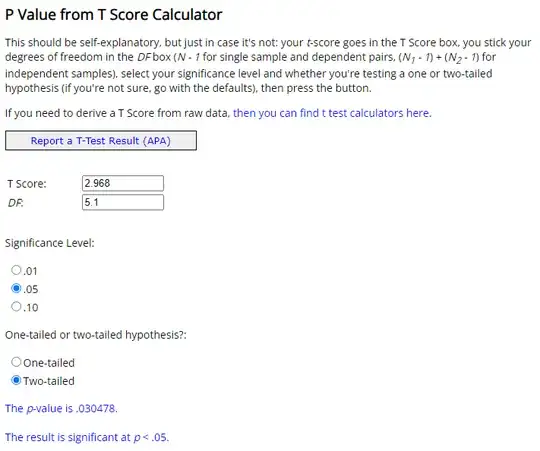
I am learning Welch's t-test and I successfully found that, in a two sample test, $t=2.968$ and the degree of freedom is $5.1$. I then go to an online p-value calculator for the p-value at 0.05 significance level. The results are as follows.

P value from Online Calculator

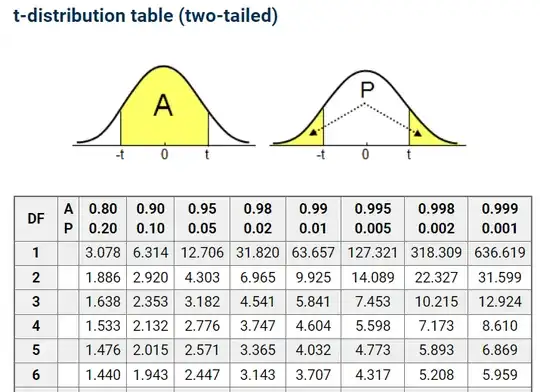
The problem is that I don't understand how the number $0.030478$ is generated. I tried to look at the two-tailed t-distribution table, but then I am not sure how to interpolate the p-value from the table. T table

Can anyone explain why $0.030478$ is the p-value here? Is it possible to get this number with the t-distribution table and a calculator only? I would like to learn how to get this number without the help of online calculator. Thanks in advance.

Am_2099
  • 107

2 Answers2

1

If you were using the R statistical programming language, you could replicate the $0.030478$ result with

> 2 * pt(2.968, df=5.1, lower.tail=FALSE)
[1] 0.03047769

which corresponds to the chart with P from your tables (the 2 * comes from using two tails).

The nearest you get to it in the numbers in your tables is that $2.968$ is between $2.571$ and $3.365$ in the $DF=5$ row, which at the top suggests a $p$-value between $0.05$ and $0.02$.

$DF=5 \not= 5.1$ but they are close, and $2.968$ is also between $2.447$ and $3.143$ in the $DF=6$ row, so combined this tells you have $0.02 < p < 0.05$ which will be seen as significant when your test uses $\alpha=0.05$.

If you really wanted to linearly interpolate as an an approximation, you could try $\frac{6-5.1}{6-5}\left(\frac{3.365-2.968}{3.365-2.571}0.05+\frac{2.968-2.571}{3.365-2.571}0.02\right) + \frac{5.1-5}{6-5}\left(\frac{3.143-2.968}{3.143-2.447}0.05+\frac{2.968-2.447}{3.143-2.447}0.02\right)$ which would give about $0.034$; this is not awful, though it is not very good either. You might use more detailed tables of the $t$ distribution, though those rarely have non-integer degrees of freedom, or preferably a statistical calculator.

Henry
  • 169,616
0

I think that stats.exchange.com may be better suited for your question. Anyway, you can compute this using a calculator if you are able to compute $$F(t) = 1-\frac 12\left(1 + \operatorname{sign}(t)\cdot I\left(\frac 12, \frac{\nu}{2}, \frac{t^2}{t^2 + \nu}\right)\right),$$ where $t$ denotes the value of your test statistic, $\nu$ denotes the degrees of freedom, $\operatorname{sign}$ is the sign function, i.e., $$\operatorname{sign}(t) = \begin{cases} 1 & \text{if $t > 0$} \\ 0 & \text{if $t = 0$} \\ -1 & \text{if $t < 0$}\end{cases},$$ and $I(x,y,z)$ is the regularized incomplete Beta function $$I(a,b,x) = \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\int_0^xy^{a-1}(1-y)^{b-1}\,\mathrm dy.$$ Here $\Gamma$ denotes the Gamma function $$\Gamma(x) = \int_0^\infty y^{x - 1}\exp(-y)\,\mathrm dy.$$ So you would need a calculator that has both the Gamma function and the incomplete regularized Beta function available. Eventually, the p-value for a two-sided test is computed as $$p = 2\min\big(F(t), 1-F(t)\big).$$

The numbers in the table are the values for $t$ for given $\nu$ and $\alpha$ with $p = 1-\alpha$.

You can infer that with your $t$, you are in the third column, and in the second last or last row as $\nu=5.1$. A (crude) approximation would a linear interpolation:

  1. We have that $\frac{2.571 - 2.447}{10}\approx 0.0124$, so $2.571 - 0.0124 \approx 2.559$ would correspond to $\alpha = 0.05$ and $\nu = 5.1$.
  2. Similarly, $3.343$ would correspond to $\alpha = 0.02$ and $\nu = 5.1$.
  3. Your test statistic is $2.968$, which is in between $2.559$ and $3.343$. Precisely, $$\frac{2.968}{2.559+3.43}\approx 0.5029.$$ Now find the corresponding value between $\alpha = 0.02$ and $\alpha = 0.05$: $$0.5029\cdot(0.02 + 0.05) \approx 0.0352.$$ The first two digits are equal, but the relative error is 15 %.
Quertiopler
  • 241