Consider sticks of lengths $f(1),f(2),f(3),\dots,f(n)$ where $f(j)=j^\text{th}$ prime number.
Here is an example with $n=50$.
Let $P(n)=$ probability that three randomly chosen sticks can form a triangle.
What is $L=\lim\limits_{n\to\infty}P(n)$ ?
I am looking for a closed form for $L$, or if there is no closed form, then an approximation.
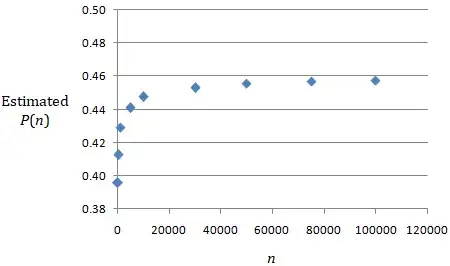
Simulations
Simulations suggest that $L\approx 0.46$.
My attempt
Suppose, for a given $n$, we have alreaday chosen $f(a)$ and $f(b)$, and we are about to choose $f(c)$.
If $f(a),f(b),f(c)$ can be the side lengths of a triangle, then $|f(a)-f(b)|<f(c)<f(a)+f(b)$, that is, $f^{-1}(|f(a)-f(b)|)<c<f^{-1}(f(a)+f(b))$.
So the probability that $f(a),f(b),f(c)$ can be the side lengths of a triangle is
$$\frac{\min\left(f^{-1}(f(a)+f(b)),n\right)-f^{-1}(|f(a)-f(b)|)}{n}$$
Then we take the average as $a$ and $b$ run from $1$ to $n$.
$$P(n)=\frac{1}{n^2}\sum_{a=1}^n\sum_{b=1}^n\frac{\min\left(f^{-1}(f(a)+f(b)),n\right)-f^{-1}(|f(a)-f(b)|)}{n}$$
If we use the prime number theorem to approximate $f(j)\approx j\log j$ and $f^{-1}(j)\approx\frac{j}{\log j}$ (which are asymptotic inverses), then
$$P\left(10^2\right)\approx 0.3595$$ $$P\left(10^3\right)\approx 0.4007$$ $$P\left(10^4\right)\approx 0.4246$$ $$P\left(10^5\right)\approx 0.4396$$
but I do not know how to take the limit as $n\to\infty$.
Context
Earlier I found that if $f(j)=j^{1/k}$ then $L=1-\dfrac{1}{\binom{2k}{k}}$, and I seeking a combinatorial proof for this fact.
Now I am wondering what $L$ is, if $f(j)=j^\text{th}$ prime number.