6

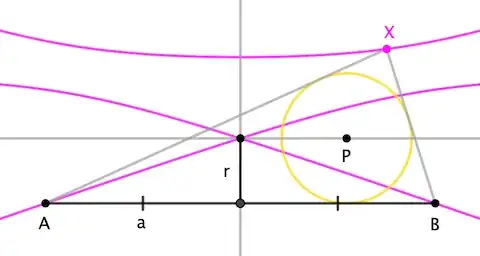
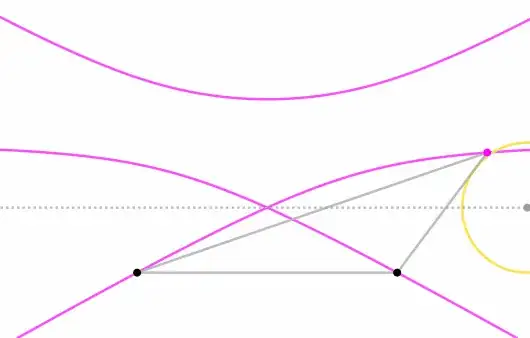
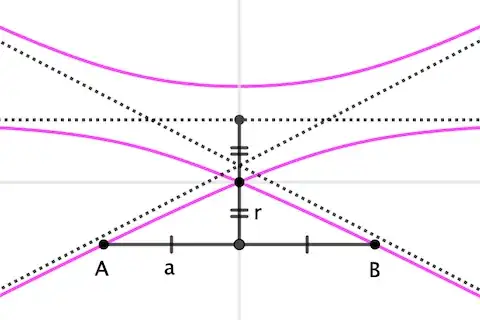
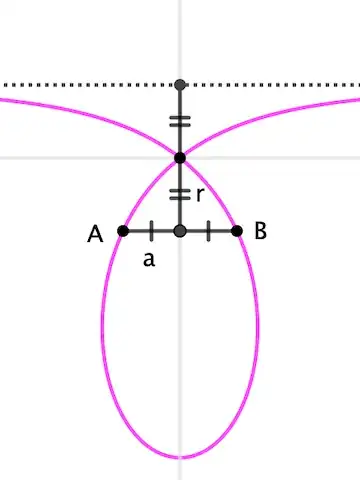
Let $r, s$ be parallel lines and $A, B$ points on $r$. Let $\Gamma$ be a circle with center on $s$ and tangent to $r$. Finally, let $X$ be the intersection point of the tangents to $\Gamma$ through $A$ and $B$ other than $r$. This is the setup I came up with by playing around on Geogebra. Now what caught my attention was the path $\gamma$ traced by the point $X$ when we let the center of the circle change over $s$.

In the image below we can see this path looks like an hyperbola. I've never seen something like this being used to describe an hyperbola before, despite this being a very simple setup, so this made me very curious. First of all, I want to know if one can show $\gamma$ is, in fact, an hyperbola (it is very clear by the image this is the case, but I'm not sure how to prove it). Second, I wonder what is its relation with the points $A, B$ and lines $r, s$. It seems $A, B$ are points on $\gamma$ and lines $r, s$ are parallel to its directrices. What else can we tell? Does it have a simple equation?

Two parallel lines r and s are shown, with points A and B on line r. A circle, Γ, tangent to line r, has its center on line s. Tangents are drawn from points A and B to the circle, intersecting at point X, which lies above the circle. The path traced by X as the center of the circle moves along line s is depicted as a hyperbola.

I just now realized there is a simpler way to describe $\gamma$. It is the locus of the third point of a triangle having a fixed incircle radius.

Alma Arjuna
  • 6,521

2 Answers2

7

Suppose $|AB|=2a$ and the circle (of variable center $P$) has radius $r$. Coordinating, we can write: $$A = (-a, -r) \qquad B = (a, -r) \qquad P = (p,0) \tag1$$ for variable $p$. With a bit of symbol-bashing in Mathematica, we find that the coordinates of point $X$ such that $\bigcirc P$ is the incircle of $\triangle ABX$ are given by $$(x,y) \;=\; \frac{a^2 + r^2 - p^2}{a^2 - r^2 - p^2} \;\left( p,r\right) \tag2$$ Eliminating parameter $p$ leaves the cubic curve $$r^2 y^2\,(r + y) \;=\;(r - y) \left(r^2 x^2 - a^2 y^2\right) \tag3$$ not a hyperbola.

cubic incircle locus

Here's an animation:

enter image description here

Note that only the upper branch ($p^2\leq a^2-r^2$) corresponds to the given circle being inscribed; elsewhere, it's escribed.

The cubic crosses the origin twice, and meets the $y$-axis again at $y= r\,\dfrac{a^2 + r^2}{a^2-r^2}$.

The cubic is asymptotic to the lines $y=r$ and $y = \pm\dfrac{rx}{\sqrt{a^2 - r^2}}+\dfrac{r^3}{a^2-r^2}$. The $y$-intercept of the obliques is halfway between the midpoint of $AB$ and the third $y$-intercept of the cubic itself.

enter image description here

When $a<r$, the cubic becomes a loop with a single asymptote.

enter image description here

Blue
  • 83,939
  • This is amazing! Can we get rid of the portion of the graph below and isolate y as a function of x? – Alma Arjuna Oct 02 '24 at 15:53
  • 1
    @AlmaArjuna: Solving the cubic equation for $y$ yields a sprawling mess. If you want to graph the curve at all, I recommend using the parametric form $(2)$; for the upper branch alone, impose the restriction $p^2<a^2-r^2$. – Blue Oct 02 '24 at 16:45
  • 1
    @Blue that will do it, thank you so much! :) – Alma Arjuna Oct 02 '24 at 18:20
  • 1
    @Blue: Apologies, forgive the nocturnal comment. – Narasimham Oct 02 '24 at 20:52
0

We assume $r$ as $x$ axis. Formula for the coordinates of the incentre of a triangle is $$\bigg(\frac{ax_1+bx_2+cx_3}{a+b+c},\frac{ay_1+by_2+cy_3}{a+b+c}\bigg)$$ where $a,b,c$ are sides opposite to angles $A,B,C$. We notice here that the $y$ coordinate of the incentre remains fixed as the radius of the circle, so we can equate it to $r$. $$\frac{ay_1+by_2+cy_3}{a+b+c}=r$$ If we take coordinates of $X$ as $(h,k)$, we get the equation $$(-r)\sqrt{(h-x_b)^2+k^2} + (-r)\sqrt{(h-x_a)^2+k^2} = (r-k)(x_b-x_a)$$

Wolfram gives a humongous answer Analysing the equation,we see both $h$ and $k$ have highest degree of $4$ in the equation, which is why the answer is so big.

Gwen
  • 3,910
  • 6
  • 19