1

This SE question has a nice answer describing how to derive the PDF of the chi-square distribution by inverting its characteristic function, in an elegant method using contour integrals.

How can we use the same contour integral method to derive the PDF of the non-central chi-square distribution, from its characteristic function:

$$\phi(t)=\frac{\exp\left(\frac{i\lambda t}{1-2it}\right)}{(1-2it)^{k/2}}$$

It is known that the resulting PDF would be in terms of the modified Bessel function of the first kind. Wikipedia says that the Bessel function can be described as a Fourier transform of 'powers of quadratic functions', which might be the link.

Abhranil Das
  • 175

1 Answers1

0

there are several papers for references.

  1. A CONTOUR-INTEGRAL DERIVATION OF THE NON-CENTRAL,CHI-SQUARE DISTRIBUTION

This paper makes full use of the residue theorem to solve this problem.

  1. ANOTHER DERIVATION OF THE NON-CENTRAL CHI-SQUARE DISTRIBUTION

The method using polar co-ordinates is quite straightforward.

  1. THE NON-CENTRAL $X^2$ AND F-DISTRIBUTIONS AND THEIR APPLICATIONS

This paper provides another view to the distribution. It explains the Poisson part in the non-central chi-squared pdf, quite interesting.

$\chi^2=\sum_{i=1}^n x_i^2 $ is distributed as $\chi^2=\sum_{i=1}^{n-1} y_i^2 + y_n^2$, the sum of the squares of (n - 1) normal variates with mean zero and the square of a single normal variate with mean $\sqrt{\lambda} $.

The degrees of freedom of the chi-squared distribution may be even or odd, the proof is slightly different. I prefer to the even degree because it is quite simple. Please refer to paper 1 mentioned above for the whole proof.

The CF function of non-central chi-squared distribution $ Y $~$ \chi^2(n,\lambda) $ is $ \phi(t) = (1-2it)^{-n/2}e^{\frac{i\lambda t}{1-2it}} $, for the inverse transform $ f(y) = \frac{1}{2\pi}\int_{-\infty}^{+\infty}(1-2it)^{-n/2}e^{\frac{i\lambda t}{1-2it}}e^{-ity}dt $. $\\$

Let the $z= 1-2it$, so $t = \frac{i}{2}(z-1), dt = \frac{i}{2}dz$ ,the integration above becomes $$ f(y) = \frac{1}{2\pi}\int_{1+i\infty}^{1-i\infty}\frac{i}{2}z^{\frac{-n}{2}}e^{\frac{-\lambda (z-1)}{2z}}e^{\frac{y(z-1)}{2}}dz = \frac{1}{2\pi}\int_{1+i\infty}^{1-i\infty}\frac{i}{2}z^{\frac{-n}{2}}e^{(\frac{-\lambda }{2} +\frac{\lambda}{2z})}e^{(\frac{yz}{2}-\frac{y}{2})}dz \\= \frac{1}{2\pi}\int_{1+i\infty}^{1-i\infty}\frac{i}{2}e^{\frac{-(y+\lambda)}{2}}e^{(\frac{\lambda}{2z}+\frac{yz}{2})}z^{\frac{-n}{2}}dz $$

expand $$e^{\frac{\lambda}{2z}} = \sum_0^\infty \frac{({\lambda /2})^m}{m!}z^{-m}$$ so $$ f(y) = \frac{1}{2\pi}\frac{i}{2}e^{\frac{-(y+\lambda)}{2}}\sum_0^\infty \frac{({\lambda /2})^m}{m!}\int_{1+i\infty}^{1-i\infty}\frac{e^\frac{yz}{2}}{z^{\frac{n}{2}+m}} dz = -\frac{1}{2\pi}\frac{i}{2}e^{\frac{-(y+\lambda)}{2}}\sum_0^\infty \frac{({\lambda /2})^m}{m!}\int_{1-i\infty}^{1+i\infty}\frac{e^\frac{yz}{2}}{z^{\frac{n}{2}+m}} dz$$ consider the contour integral: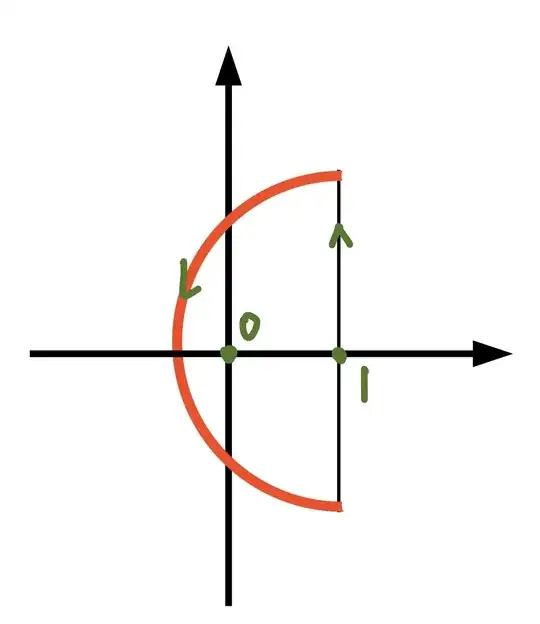enter image description here $f(y)$ is the black one, the red one can be proved to be zero easily.

Let $z=re^{i \theta}, \theta \in(\frac{\pi}{2}, \frac{3\pi}{2})$, the integrand $$\frac{e^\frac{yz}{2}}{z^{\frac{n}{2}+m}} = \frac{e^{\frac{y}{2}r({cos\theta+isin\theta})}}{r^{(n/2+m)}e^{i\theta(n/2+m)}} = \frac{e^{\frac{y}{2}(r{cos\theta})}e^{\frac{y}{2}(ir{sin\theta})}}{r^{(n/2+m)}e^{i\theta(n/2+m)}} \rightarrow zero $$ because $cos\theta < 0$, $e^{\frac{y}{2}(r{cos\theta})}\rightarrow 0 $ as $r\rightarrow\infty$, and $r^{(n/2+m)}$ $\rightarrow \infty$ when $r\rightarrow\infty$, finally, the integrand equals $\frac{0}{\infty}\rightarrow 0$

so apply the residue theorem $$ f(y) = -\frac{1}{2\pi}\frac{i}{2}e^{\frac{-(y+\lambda)}{2}}\sum_0^\infty \frac{({\lambda /2})^m}{m!} \frac{2\pi i}{({\frac{n}{2}}+m-1)!}{{(\frac{y}{2})}^{\frac{n}{2}+m-1}} $$ if the degree n is even, then $(\frac{n}{2}+m-1)! = \Gamma (\frac{n}{2}+m)$

so $$f(y) = \frac{y^{\frac{n}{2}-1}e^\frac{-(y+\lambda)}{2}}{2^\frac{n}{2}}\sum_0^\infty \frac{({\frac{\lambda y}{4}})^m}{m!\Gamma (\frac{n}{2}+m)} $$

Hermann
  • 51