Why the derivatives $f^{(n)}(x)$ of Flat functions grows so fast? (intuition behind)

Question

Why the derivatives $f^{(n)}(x)$ of Flat functions grows so fast? (intuition behind)

In this other question I did about Bump functions, other user told in an answer that these kind of functions "tends aggressively fast to zero at the limits of the support", and it keeps in my mind trying to understand what this is supposedly means:

From one side, the functions speed, acceleration, and any other derivatives are bounded since these functions are smooth $C_{c}^{\infty}$, which implies that is completely the opposite was being proposed, the speed and acceleration is finite as any other derivatives, and they looks being well-behaved functions as you expect for something smooth (at least for me, since I relate smooth with polynomials).

But on the other hand, this user and his answer has a point: I have noticed that as I take increasing order derivatives of Flat functions like Bump functions, their higher derivatives maximum values start increasing very fast $\|f^{(n)}(x)\|_{\infty}$ as $n$ grows, and as I understood the formulas, I don't get the intuition behind it.

For me its very counter-intuitive that something that is becoming a constant with bounded speed ($\|f^{(1)}(x)\|_{\infty} \ll \infty$) somehow have higher derivatives are kind of blowing up, which is even more weird in the case of Bump functions since they are smooth $C_{c}^{\infty}$. And with becoming a constant, I mean that for continuously becoming flat all the derivatives must becomes zero at these special inflection points $x^*$ since $\frac{d^n}{dx^n}f(x)\Biggr|_{x\to {x^*}^{\pm}}=0,\,n\geq 1,\, n\in \mathbb{Z}$.

As example, for polynomials as I increase the order of their derivatives, they start to approach to a straight line as their constituent polynomial reduce is order (at least until you match the order of the polynomial), but instead in Flat functions they start to blowing up similarly to what happens when taking $n^{th}$-differences among samples of a Brownian motion, which are in converse very irregular nowhere-differentiable continuous functions (they are actually example of pathological functions, but also as are Flat functions since they aren't analytical in their full domains - check Non-analytic smooth function).

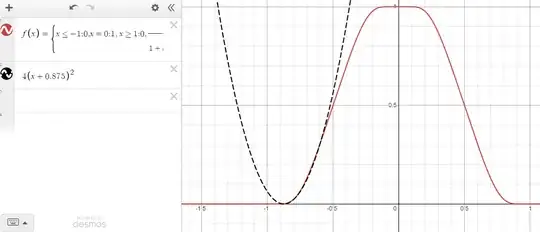
To use a simple example as common ground for the answers let think of this one: $$f(x) = \begin{cases} 0,\quad x\leq -1;\\ 0,\quad x\geq 1;\\ 1,\quad x=0;\\ \dfrac{1}{1+\exp\left(\frac{1-2|x|}{x^2-|x|}\right)},\quad\text{otherwise;} \end{cases}$$ You can check the plot of $f(x)$ in Desmos.

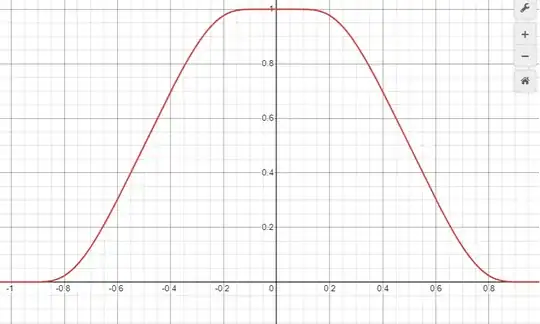
Their first derivatives' uniform norms are: $$\|f(x)\|_{\infty} = 1;\quad \|f'(x)\|_{\infty} = 2;\quad \|f''(x)\|_{\infty} \approx 9.84;\quad \|f^{(3)}(x)\|_{\infty} \approx 110.56;\quad \|f^{(4)}(x)\|_{\infty} \approx 2,280.4$$ As you could check in Desmos. As you could see they grow very fast, I tried to make a plot $n\,\text{vs}\|f^{(n)}\|_{\infty}$ and its becomes somehow linear only when applying $\ln(1+\ln(1+\|f^{(n)}\|_{\infty}))$ so I think it grows even greater than exponential, all this even when, at least visually, they look quite smooth and even comparable with a traditional quadratic decay (plot), so behaving as normal as traditional polynomials do:

So I would like to know What is actually happening here on this specific points the functions become flat, since I have arguments, I think, opposite from each other being true both at the same time, so I hope you could help me un improve my intuition about this situation.

PS: I use a lot of non-accurate meanings of some terms which I have indicated with italics, this as I am trying to improve the intuition behind and not just a formal formulation. I hope you answers also could focus in the intuition (that why I used the soft-question tag), but also formal demonstration are welcomed: my knowledge in modern abstract math is very limited (for not saying null), so please try to kept the answers at a level of undergraduate engineering courses if possible. Thanks you beforehand.

---

Added later

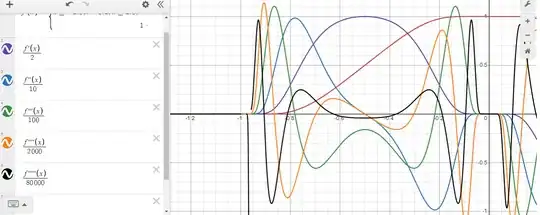
After the comment by @MartinR, I checked where the peaks of the higher order derivatives are located (I scaled them in order to be comparable) Desmos, and they start to approach the points when the flat function became zero, so there is almost no amplitude there and the slope is even lower than the slope of the function $y(x)=x$:

Since the speed is almost zero there, I am tempted to say that the situation is more like a mathematical artifact than saying "tends aggressively fast to zero" near the flat points, which could be seen because $f'(x) \approx 0$ near that neighborhood: Would you agree with that? Or are there some important technical thing I am missing with this interpretation?

I understand the rate of growth of $f(x)$ when rising from zero is nice since $\|f′(x)\|_{\infty}$ is low, but for these almost zero values near flat points, I am not sure if somehow $f(x)$ is growing faster that what any line polynomial of order $n\geq 2$ could achieve on such a short distance, but not meaning is fast as speed since just $y(x)=|x+x^*|$ rises faster than $f(x)|_{x\to x^*}$ at flat point $x^*$ (but I believe this intuition is also wrong, since each derivative peak happen at different points). Hope you could explain it.

---

2nd update

After the answer by @LorenzoPompili looks I have a confusion about the growth rate and the decay rate (which I haven't solve yet).

Which is clear to me is that the rise from zero is not infinitely fast since $f'(x)$ is quite low always.

But about the decay rate I don't know if I am "confusing the map with the territory": I am trying to understand if there is a true aggressive decay, of instead, the power series (analytical) description have limitations that don't allow to properly describe this kind of functions, don't meaning these flat function by itself are aggressively fast.

In simple words: or they have indeed aggressive decay, or instead a power series is behaving like a long wood stick that cannot match some curvy figure, if I pressed it too much, it would broke, or instead it would detach from other points they have to also fit but far away from where I am applying pressure (think of making a wooden boat).

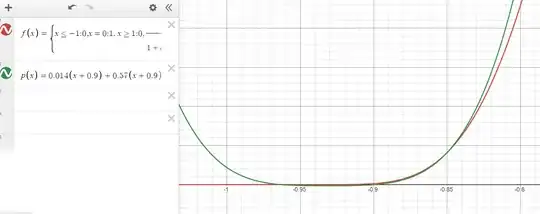
I am inclined to believe in the "wood" idea, because if I compare the function $f(x)$ near the first flat point $x^*=-1$ with the following polynomial: $$p(x) = 0.014(x+0.9)+0.57(x+0.9)^2+11.3(x+0.9)^3+91.8(x+0.9)^4$$ which is a modified version of a Taylor series at $x=0.9$. As it could be seen in Desmos it decays faster than $f(x)$ since start above it (this from right to left), matches the function $f(x)$, and then becomes zero before $f(x)$.

So in this sense a polynomial decays faster (nothing weird so far). Other story is that a power series would not be able to match perfectly the function since it would struggle in becoming flat: from one point of view is acting the Identity Theorem against it, while in the other hand the Stone–Weierstrass theorem tells I could use a polynomial as close as required to approximate it.

So I don't know which one is going to win: the first one says its imposible to match so is defending the point of view of aggressive decay, but the second one tells you that a polynomial decay would always be able to match it as close as desire, on line with the polynomial $p(x)$ comparison.

Now, I could make a truly aggressive decay by introducing a constant $n\geq 1$ on $f(x)$ as: $$f_n(x) = \begin{cases} 0,\quad x\leq -1;\\ 0,\quad x\geq 1;\\ 1,\quad x=0;\\ \dfrac{1}{1+\exp\left(\dfrac{n(1-2|x|)}{x^2-|x|}\right)},\quad\text{otherwise;} \end{cases}$$

Which behaves as a smooth approximation of the Rectangular function as $n\to\infty$. Checking the previous plot with the higher derivatives scaled new Desmos, while I increase the value of $n$ the higher derivative's peaks start moving from the flat point to where the slope is increasing near $x=\frac12$, but I am not sure if it means that the flat point is becoming irrelevant (somehow supporting the "wood" argument), or if instead it is moving into the point $x=\frac12$ where now it is kind-of rising from zero.

As you could see I still trying to understand, @LorenzoPompili gave an amazing answer but I am still lost on the details, while I think the "wood" argument is what stands, I do hope the aggressive decays is what is really happening (I think the last one is what @LorenzoPompili is telling me, from what I am understanding so far), since having that kind of restriction for rising from a position of flatness could be a good argument for dismissing self-rising solutions, like the one that happen on the Norton's Dome example, like there is an infinite inertia against start moving from zero just by itself. If there really is a connection, please try to elaborate into it.

Answer 1

Here is some intuition. Let me change variables so that $f$ is zero for negative $x$, and positive for positive $x$, and “flat” at $x=0$. By flat, I mean that all derivatives are zero.

Imagine the set of derivatives of $f$ is a happy family, and they all “start” with value zero at time $x=0$ ($f$ is flat). What they do is that the larger their value is, the faster the previous derivative is allowed to increase its value (by definition). Imagine that you are the $1000$-th derivative, and your plan is to “accelerate” $f$ so that it grows tall enough by the end of the working shift: say, you want $f(1)=1$. In order to achieve that, you know that $f’$ must increase first (because it’s zero at $x=0$), and then it has to keep an average value of $1$ on the interval $[0,1]$ ($\int_0^1 f’=f(1)$). And $f’$ has to grow rather quickly to do that: it should reach the value $1$ in due time, say, around $x=1/2$.

Ok, you see where this is going… If $f’$ needs to do the above, then $f’’$ has to wake up and kick in in due time as well, because then it can allow $f’$ to grow. But wait… Now it has even less time than the time $f’$ had to do the exact same thing, because we want $f’(x)=1$ at around $x=1/2$. So, $f’’$ has to wake up and start working even earlier than $f’$. And not only that! Since it has less time, it needs to keep an average value of $2$ on the interval $[0,1/2]$, so it must reach $2$ at around $x=1/4$.

Oh no… This means that the third derivative has even less time, so it has to wake up even earlier, and work with much more intensity than $f’’$. It will have to reach $4$ at $x=1/8$.

…

So if you are the $1000$-th derivative, you will have to kick in almost immediately and increase to an incredible magnitude in order to make $f^{(999)}$ grow, which later will make $f^{(998)}$ grow, which later will make $f^{(997)}$ grow…

This is the main intuition. The rough numbers are even too optimistic, because it assumes that all derivatives can grow roughly linearly, but they actually grow much slower. So in the end you get that superexponential growth, which should be the $n!$ that pops up in Taylor’s theorem.

Edit. In fact, a rigorous version of the above argument is basically just the proof of Taylor's theorem. You have $$f(1)=\int_0^1 f'(s)ds.$$ Integrating by parts once, you get $$ f(1)=\int_0^1 (1-s)f''(s)ds. $$ Integrating by parts multiple times, you get $$ f(1)=\frac{1}{(n-1)!}\int_0^1 (1-s)^{n-1}f^{(n)}(s)ds. $$ $$\implies |f(1)|\leq\frac{1}{(n-1)!}\int_0^1 (1-s)^{n-1}ds\|f^{(n)}\|_{L^\infty}=\frac{1}{n!}\|f^{(n)}\|_{L^\infty}.$$ The boundary data all vanish because $f$ and its derivatives are zero at $x=0$, and $(1-x)^k$ is zero at $x=1$. So, the contribution of the $n$-th derivative to the value of $f(1)$ is incredibly small. To make $f$ grow, the $n$-th derivative has to be incredibly large.

You can see a finite version of this phenomenon with polynomials. The $n$-th derivative of $x^n$ is $n!$, extremely large for large $n$. This has to be like that, because all derivatives up to order $n-1$ of $x^n$ vanish at $x=0$, and the same argument as above applies.

---

So I would say that even if it sounds strange that derivatives “have to blow up”, it could be helpful thinking that pushing a function up from the high order derivatives is like pushing a rock with incredibly huge inertia, which is initially still because all the derivatives are zero at $x=0$.

---

Edit.

Let me address the "aggressive" sentence you mentioned. I personally think that both sentences "tends aggressively fast to zero" and "tends very slowly to zero" apply to a flat function $f$ without contradiction. It really depends what you mean there by "fast" and "slow". If you mean fast as "high slope", then I agree that flat functions converge very slowly to zero. But in the first sentence, "fast" means something different.

To illustrate what I mean, let's use a logarithmic change of variables.

For a function $f:(0,\infty)\to (0,\infty)$, let $$ F(\tau):=\log(f(e^{\tau})). $$ The behaviour of $f$ at zero corresponds to the behaviour of $F$ at $-\infty$.

If $g(x)=x^n$, you have $G(\tau)=n\tau$. So for functions that decay polinomially at zero, after changing variables they decay linearly as $\tau\to-\infty$.

If you plug $f(x)=e^{-1/x}$, which is flat at zero (extending it as zero for negative $x$) you get $$ F(\tau)=-e^{-x} $$ which decays exponentially as $x\to-\infty$. With these new variables, you can really see that the convergence of $f$ to zero gets very "fast" when you are close to $x=0$. You see that "fast" mean different things when you change point of view.

Now you may say "Ok man, but you have used an arbitrary change of variables. Your notion of "fast" might depend on the change of variable you use". A legitimate objection. So, in which sense I am saying that this convergence is "fast"? I would describe it rigorously in the following way: as $x\to 0+$, $f(x)$ escapes all compact subsets of $(0,\infty)$ with a rate that is very fast. Or, say, $f(x)$ enters all neighbourhoods of zero with a rate that is very fast. For example, if you choose a sequence of neighbourhoods of zero like $$ U_n=(-2^{-n},2^{-n}) $$ and a sequence of points $x_n\to 0$ like $x_n=2^{-n}$, you have that the sequence $f(x_n)$ enters all sets $U_n$, with a rate that is extremely fast, faster than say $g(x)=x^n$, for any $n$.

Another way of looking at it. For any $n\geq 0$, $ f(x)/x^n $ converges to zero as $x\to 0$, so $f$ has to reach zero with a "faster rate", in the sense that it gets much, much closer to zero than $g$ eventually.

This is what people in math think when they say that flat functions converge very fast to zero. This of course implicitly assumes that small scales are equally important to large scales. If you don't care too much about small scales, then this notion is meaningless. But as I said in a comment below, if you consider not meaningful what the function does at small scales, then it is also meaningless to look at pointwise evaluation of derivatives with very high order.