4

Let $f: [0,{\infty}) \to[0,{\infty})$ be a continuous function.

If $ \int_0^{\infty}f(x)<{\infty}$, then $\int_0^{\infty}{f(x)}^2<{\infty} $

Is the statement true?
My approach: At first, I was thinking of this example

$f(x) = \begin{cases} \frac{1}{x^{1/2}}, & x \in (0,1) \\ 0, & \text{otherwise} \end{cases} $

then, $\int_0^{1}\frac1{x^{1/2}}dx<{\infty}$
and $\int_0^{1}(\frac1{x^{1/2}})^2dx=\int_0^{1}\frac1xdx$ diverges.
But the function f is not continuous in $[0,\infty)$.Any hint would be appreciated.

Curious One
  • 99
  • 4
    Have you tried examples? Edit your post to include your efforts. – Ted Shifrin Aug 23 '24 at 16:20
  • 1
    This is an interesting problem but a poor question. You need to give some background to your asking of the question and show some of your thoughts/work to bring it up to the standards of the site. For a hint that would answer the question for some people: $$\sum \frac{2^n}{4^n}< \infty \ \sum \frac{(2^n)^2}{4^n} = \infty$$ – Brian Moehring Aug 23 '24 at 16:32
  • $L^2\subset L^1$ only in finite measure spaces (which $[0,\infty)$ , under the standard measure, is not.) A counterexample is $$f(x)=\frac{1-\operatorname{smoothstep}(x-1)}{\sqrt x}$$ Where $\operatorname{smoothstep}$ denotes the smoothstep function. – K.defaoite Aug 23 '24 at 17:33
  • 1
    @K.defaoite Two points. (1) Whether $L^2\subset L^1$ or not doesn't matter here. The question is more akin to the reverse direction (which in full generality fails even if we have a finite measure space). (2) Your proposed example doesn't work. What would $f(0)$ be to make $f$ continuous? – Brian Moehring Aug 23 '24 at 20:32
  • 3
    Now that the op has edited their efforts, this post does not deserve downvotes anymore. – Mr. Gandalf Sauron Aug 24 '24 at 08:11
  • 1
    Apparently $\int_0^\infty e^{-x}/\sqrt {x}$ converges but the square does not – Chris Aug 24 '24 at 08:57
  • @Chris is it continuous at x=0? – Curious One Aug 24 '24 at 09:10
  • @CuriousOne The main thing is that the function must be bounded in any compact interval and uniformly continuous there. That's why letting examples which are $L^{2}$ but not $L^{1}$ in a finite measure space won't suffice. You'll have to go for functions which are $L^{\infty}$ and uniformly continuous in any compact interval, but it is unbounded in $\Bbb{R}$. – Mr. Gandalf Sauron Aug 24 '24 at 09:30
  • You guys are right, I missed the continuous at $0$ part of the question. – Chris Aug 24 '24 at 09:37
  • Related – Sine of the Time Aug 24 '24 at 09:40

1 Answers1

7

Firstly, you have to ensure that $f(x)$ does not tend to $0$ as $x\to\infty$ uniformly. Because then, after a certain $M$, $f(x)<1$ for all $x\geq M$ and hence, $f(x)^{2}$ will have a faster decay and hence $\int_{M}^{\infty}f(x)^{2}\,dx\leq \int_{M}^{\infty}f(x)\,dx<\infty$. And $f$ will be uniformly bounded on $[0,M]$ and hence integrable.

The way to construct a counter-example is by using pictures.

Let $f(x)=0$ for $x\in[0,1]$.

For $x\geq 1$, for each $n\geq 1$, in the interval $[n,n+\frac{1}{n^{3}}]$, let $f(n)=0, f(n+\frac{1}{2n^{3}})=n$ and $f(n+\frac{1}{n^{3}})=0$ and we linearly interpolate between these points. And let $f$ be $0$ elsewhere. Then $f$ is easily continuous as it is formed by linear interpolations.

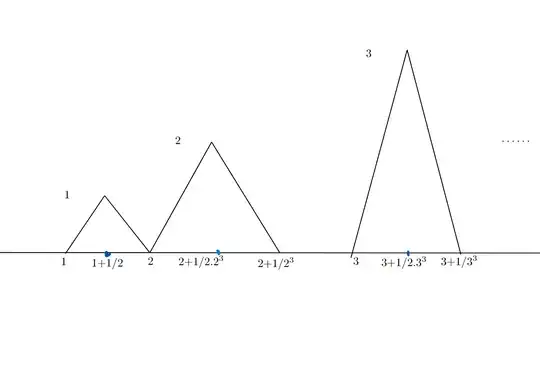
enter image description here

(Note that the triangles may not appear symmetric. That is because I am bad at drawing).

The idea is that you are constructing triangles with unbounded heights but with fast enoguh diminishing base lenghts. The base of the triangles are formed by the interval $[n,n+\frac{1}{n^{3}}]$ and the height of the triangle is $n$, i.e. $f(n+\frac{1}{2n^{3}})=n$

So $\int_{0}^{\infty}f(x)\,dx=\sum_{n}\text{Area of the nth-triangle}=\sum_{n}\frac{1}{2}\cdot n\cdot\frac{1}{n^{3}}<\infty$

But, now note that for $x\in [n,n+\frac{1}{2n^{3}}]$, $f(x)=2\cdot(n^{4}x-n^{5})$

So \begin{align}\int_{0}^{\infty}f(x)^{2}\,dx&=\sum_{n}2\cdot \int_{n}^{n+\frac{1}{2n^{3}}}4(n^{4}x-n^{5})^{2}\,dx\\\\&=\sum_{n}\frac{8}{3n^{4}}\bigg(n^{4}(n+\frac{1}{2n^{3}})-n^{5}\bigg)^{3}\\\\&=\sum_{n}\frac{8}{3n^{4}}\cdot\left(\frac{n}{2}\right)^{3}\\\\ &=\sum_{n}\frac{1}{3n}=\infty\end{align}

Mr. Gandalf Sauron
  • 17,114