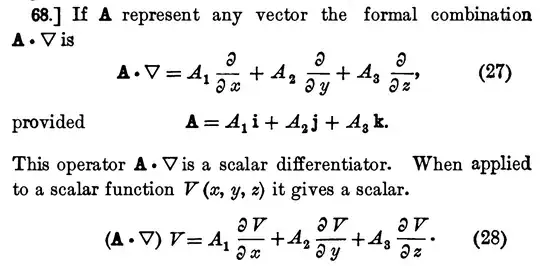Gradient of a dot product

Question

The wikipedia formula for the gradient of a dot product is given as

$$\nabla(a\cdot b) = (a\cdot\nabla)b +(b\cdot \nabla)a + a\times(\nabla\times b)+ b\times (\nabla \times a)$$

However, I also found the formula $$\nabla(a\cdot b) = (\nabla a)\cdot b + (\nabla b)\cdot a $$

So... what is going on here? The second formula seems much easier. Are these equivalent?

Answer 1

They are basically the same. For the first identity, you could refer to my proof using Levi-Civita notation here. And for the second, you should know that $\nabla a=\left(\frac{\partial a_j}{\partial x_i}\right)=\left(\frac{\partial a_i}{\partial x_j}\right)^T$ is a matrix and dot product is exactly matrix multiplication. So the proof is $$(\nabla a)\cdot b+(\nabla b)\cdot a=\left(\frac{\partial a_j}{\partial x_i}b_j+\frac{\partial b_j}{\partial x_i}a_j\right)e_i=\frac{\partial(a_jb_j)}{\partial x_i}e_i=\nabla(a\cdot b)$$

Answer 2

Since there are not many signs that one may easily use in mathematical notations, many of these symbols are overloaded. In particular, the dot "$\cdot$" is used in the first formula to denote the scalar product of two vector fields in $\mathbb R^3$ called $a$ and $b$, while in the second formula it denotes the usual product of the functions $a$ and $b$. This means that both formulae are valid, but each one is so only in its proper context.

(It is scary to see that the answers and comments that were wrong collected the most votes!)

Answer 3

The second equation presented by you, $\boldsymbol{\nabla} \bigl( \boldsymbol{a} \cdot \boldsymbol{b} \bigr) = \: \bigl( \boldsymbol{\nabla} \boldsymbol{a} \bigr) \! \cdot \boldsymbol{b} \, + \: \bigl( \boldsymbol{\nabla} \boldsymbol{b} \bigr) \! \cdot \boldsymbol{a}$, is the primary one and it is pretty easy to derive (*

*) here I use the same notation as I did in my previous answers divergence of dyadic product using index notation and Gradient of cross product of two vectors (where first is constant)

$$\boldsymbol{\nabla} \bigl( \boldsymbol{a} \cdot \boldsymbol{b} \bigr) \! \, = \, \boldsymbol{r}^i \partial_i \bigl( \boldsymbol{a} \cdot \boldsymbol{b} \bigr) \! \, = \, \boldsymbol{r}^i \bigl( \partial_i \boldsymbol{a} \bigr) \! \cdot \boldsymbol{b} \, + \, \boldsymbol{r}^i \boldsymbol{a} \cdot \bigl( \partial_i \boldsymbol{b} \bigr) \, = \: \bigl( \boldsymbol{r}^i \partial_i \boldsymbol{a} \bigr) \! \cdot \boldsymbol{b} \, + \, \boldsymbol{r}^i \bigl( \partial_i \boldsymbol{b} \bigr) \! \cdot \boldsymbol{a} \, =$$ $$= \: \bigl( \boldsymbol{\nabla} \boldsymbol{a} \bigr) \! \cdot \boldsymbol{b} \, + \, \bigl( \boldsymbol{\nabla} \boldsymbol{b} \bigr) \! \cdot \boldsymbol{a}$$

Again, I use the expansion of nabla as linear combination of cobasis vectors with coordinate derivatives ${\boldsymbol{\nabla} \! = \boldsymbol{r}^i \partial_i}$ (as always ${\partial_i \equiv \frac{\partial}{\partial q^i}}$), the product rule for $\partial_i$ and the commutativity of dot product of any two vectors (for sure, coordinate derivative of some vector $\boldsymbol{w}$, $\partial_i \boldsymbol{w} \equiv \frac{\partial}{\partial q^i} \boldsymbol{w} \equiv \frac{\partial \boldsymbol{w}}{\partial q^i}$, is a vector and not some more complex tensor) – here ${\boldsymbol{a} \cdot \bigl( \partial_i \boldsymbol{b} \bigr) = \bigl( \partial_i \boldsymbol{b} \bigr) \cdot \boldsymbol{a}}$. Again, I swap multipliers to get full nabla $\boldsymbol{\nabla}$ at the second term

For your first equation, the one with cross products, I need to mention the completely asymmetric isotropic Levi-Civita (pseudo)tensor of third complexity, ${^3\!\boldsymbol{\epsilon}}$

$${^3\!\boldsymbol{\epsilon}} = \boldsymbol{r}_i \times \boldsymbol{r}_j \cdot \boldsymbol{r}_k \; \boldsymbol{r}^i \boldsymbol{r}^j \boldsymbol{r}^k = \boldsymbol{r}^i \times \boldsymbol{r}^j \cdot \boldsymbol{r}^k \; \boldsymbol{r}_i \boldsymbol{r}_j \boldsymbol{r}_k$$

or in orthonormal basis with mutually perpendicular unit vectors $\boldsymbol{e}_i$

$${^3\!\boldsymbol{\epsilon}} = \boldsymbol{e}_i \times \boldsymbol{e}_j \cdot \boldsymbol{e}_k \; \boldsymbol{e}_i \boldsymbol{e}_j \boldsymbol{e}_k = \;\epsilon_{ijk}\! \boldsymbol{e}_i \boldsymbol{e}_j \boldsymbol{e}_k$$

(some more details about this (pseudo)tensor can be found at Question about cross product and tensor notation)

Any cross product, including “curl” (a cross product with nabla), can be represented via dot products with the Levi-Civita (pseudo)tensor (**

**) it is pseudotensor because of $\pm$, being usually assumed “$+$” for “left-hand” triplet of basis vectors (where ${\boldsymbol{e}_1 \times \boldsymbol{e}_2 \cdot \boldsymbol{e}_3 \equiv \;\epsilon_{123} \: = -1}$) and “$-$” for “right-hand” triplet (where ${\epsilon_{123} \: = +1}$)

$$\pm \, \boldsymbol{\nabla} \times \boldsymbol{b} = \boldsymbol{\nabla} \cdot \, {^3\!\boldsymbol{\epsilon}} \cdot \boldsymbol{b} = {^3\!\boldsymbol{\epsilon}} \cdot \! \cdot \, \boldsymbol{\nabla} \boldsymbol{b}$$

For the pair of cross products that “pseudo” is compensated. As the very relevant example

$$\boldsymbol{a} \times \bigl( \boldsymbol{\nabla} \! \times \boldsymbol{b} \bigr) = \boldsymbol{a} \cdot \, {^3\!\boldsymbol{\epsilon}} \cdot \, \bigl( \boldsymbol{\nabla} \cdot \, {^3\!\boldsymbol{\epsilon}} \cdot \boldsymbol{b} \bigr) = \boldsymbol{a} \cdot \, {^3\!\boldsymbol{\epsilon}} \cdot \, \bigl( {^3\!\boldsymbol{\epsilon}} \cdot \! \cdot \, \boldsymbol{\nabla} \boldsymbol{b} \bigr) = \boldsymbol{a} \cdot \, {^3\!\boldsymbol{\epsilon}} \cdot {^3\!\boldsymbol{\epsilon}} \cdot \! \cdot \, \boldsymbol{\nabla} \boldsymbol{b}$$

Now I’m going to dive into components, and I do it by measuring tensors using some orthonormal basis (${\boldsymbol{a} = a_a \boldsymbol{e}_a}$, ${\boldsymbol{b} = b_b \boldsymbol{e}_b}$, ${\boldsymbol{\nabla} \! = \boldsymbol{e}_n \partial_n}$, ...)

$$\boldsymbol{a} \cdot \, {^3\!\boldsymbol{\epsilon}} \cdot {^3\!\boldsymbol{\epsilon}} \cdot \! \cdot \, \boldsymbol{\nabla} \boldsymbol{b} = a_a \boldsymbol{e}_a \; \cdot \epsilon_{ijk}\! \boldsymbol{e}_i \boldsymbol{e}_j \boldsymbol{e}_k \; \cdot \epsilon_{pqr}\! \boldsymbol{e}_p \boldsymbol{e}_q \boldsymbol{e}_r \cdot \! \cdot \, \boldsymbol{e}_n \left( \partial_n b_b \right) \boldsymbol{e}_b = a_a \! \epsilon_{ajk}\! \boldsymbol{e}_j \!\epsilon_{kbn}\! \left( \partial_n b_b \right)$$

There’s a relation (too boring to derive it one more time) for contraction of two Levi-Civita tensors, saying

$$\epsilon_{ajk} \epsilon_{kbn} \: = \: \bigl( \delta_{ab} \delta_{jn} \! - \delta_{an} \delta_{jb} \bigr)$$

Thence

$$a_a \! \epsilon_{ajk} \epsilon_{kbn}\! \left( \partial_n b_b \right) \boldsymbol{e}_j = \, a_a \bigl( \delta_{ab} \delta_{jn} \! - \delta_{an} \delta_{jb} \bigr) \! \left( \partial_n b_b \right) \boldsymbol{e}_j = \, a_a \delta_{ab} \delta_{jn} \! \left( \partial_n b_b \right) \boldsymbol{e}_j - a_a \delta_{an} \delta_{jb} \! \left( \partial_n b_b \right) \boldsymbol{e}_j =$$ $$= \, a_b \! \left( \partial_n b_b \right) \boldsymbol{e}_n - \, a_n \! \left( \partial_n b_b \right) \boldsymbol{e}_b = \left( \boldsymbol{e}_n \partial_n b_b \right) a_b - \, a_n \! \left( \partial_n b_b \boldsymbol{e}_b \right) = \left( \boldsymbol{e}_n \partial_n b_b \boldsymbol{e}_b \right) \cdot a_a \boldsymbol{e}_a - \, a_a \boldsymbol{e}_a \! \cdot \left( \boldsymbol{e}_n \partial_n b_b \boldsymbol{e}_b \right)$$

Back to the direct invariant tensor notation

$$\left( \boldsymbol{e}_n \partial_n b_b \boldsymbol{e}_b \right) \cdot a_a \boldsymbol{e}_a = \: \bigl( \boldsymbol{\nabla} \boldsymbol{b} \bigr) \! \cdot \boldsymbol{a}$$

$$a_a \boldsymbol{e}_a \! \cdot \left( \boldsymbol{e}_n \partial_n b_b \boldsymbol{e}_b \right) = \boldsymbol{a} \cdot \bigl( \boldsymbol{\nabla} \boldsymbol{b} \bigr)$$

Sure, the latter one can also be written as

$$\boldsymbol{a} \cdot \bigl( \boldsymbol{\nabla} \boldsymbol{b} \bigr) \! \, = \, a_a \boldsymbol{e}_a \! \cdot \left( \boldsymbol{e}_n \partial_n b_b \boldsymbol{e}_b \right) \, = \, \left( a_a \boldsymbol{e}_a\! \cdot \boldsymbol{e}_n \partial_n \right) b_b \boldsymbol{e}_b \, = \: \bigl( \boldsymbol{a} \cdot \boldsymbol{\nabla} \bigr) \boldsymbol{b}$$

And finally (***

***) it looks like meanwhile I also answered to Formula of the gradient of vector dot product

$$\boldsymbol{a} \times \bigl( \boldsymbol{\nabla} \! \times \boldsymbol{b} \bigr) = \: \bigl( \boldsymbol{\nabla} \boldsymbol{b} \bigr) \! \cdot \boldsymbol{a} \: - \: \boldsymbol{a} \cdot \bigl( \boldsymbol{\nabla} \boldsymbol{b} \bigr)$$

or

$$\boldsymbol{a} \times \bigl( \boldsymbol{\nabla} \! \times \boldsymbol{b} \bigr) = \: \bigl( \boldsymbol{\nabla} \boldsymbol{b} \bigr) \! \cdot \boldsymbol{a} \: - \: \bigl( \boldsymbol{a} \cdot \boldsymbol{\nabla} \bigr) \boldsymbol{b}$$

or

$$\bigl( \boldsymbol{\nabla} \boldsymbol{b} \bigr) \! \cdot \boldsymbol{a} = \: \bigl( \boldsymbol{a} \cdot \boldsymbol{\nabla} \bigr) \boldsymbol{b} \: + \: \boldsymbol{a} \times \bigl( \boldsymbol{\nabla} \! \times \boldsymbol{b} \bigr)$$

I hope now it’s easy enough for everyone to get similar relations for $\bigl( \boldsymbol{\nabla} \boldsymbol{a} \bigr) \! \cdot \boldsymbol{b}$ and “yes” for question Are these equivalent?

Answer 4

Let us use the following index and shorthand notation. $u_{,i}=\displaystyle{\frac{\partial u}{\partial x_i}}$ . $x_1=x ,x_2=y, x_3=z$. Einstein notation. Repeated index means summation over it, and $[.]_i$ the i-th compnent of whatever is inside the square brackets $[]$.

Then \begin{eqnarray} [\nabla (\mathbf{a} \cdot \mathbf{b})]_i = (a_j b_j)_{,i} = a_{j,i}b_j + a_j b_{j,i}. \end{eqnarray}

That is all, I do not see anything more complicated than this. The two sums are matrix vector multiplications. Note that $a_{j,i} b_j$ means the matrix $\partial a_j/\partial x_i$ times the vector $b_j$. You can write this in two different forms \begin{eqnarray} (\nabla \mathbf{a}) \cdot \mathbf{b}= (\mathbf{b} \cdot \nabla) \mathbf{a} = \left ( \begin{array}{c} \displaystyle{b_1 \frac{\partial a_1}{\partial x} + b_2 \frac{\partial a_1}{\partial y} + b_ 3 \frac{\partial a_1}{\partial z}} \\ \\ \displaystyle{b_1 \frac{\partial a_2}{\partial x} + b_2 \frac{\partial a_2}{\partial y} + b_3 \frac{\partial a_2}{\partial z}} \\ \\ \displaystyle{b_1 \frac{\partial a_3}{\partial x} + b_2 \frac{\partial a_3}{\partial y} + b_3 \frac{\partial a_3}{\partial z}} \end{array} \right ) \end{eqnarray} Where the symbol $\nabla \mathbf{a}$ means a matrix. The matrix whose rows are gradients of the components $a_1,a_2,a_3$ respectively. To be more precise the vector $\mathbf{b}$ on the left side is a column vector and that on the center is a row vector, so we can call the vector on the center instead $\mathbf{b}^T$ or transposed of the column vector $\mathbf{b}$, the whole expression in the center should be transposed as well...but this is a minor detail. I do not see any difference between these two things. So we can say \begin{eqnarray} \nabla (\mathbf{a} \cdot \mathbf{b}) = (\nabla \mathbf{a}) \cdot \mathbf{b} + \mathbf{a} \cdot \nabla \mathbf{b} = (\mathbf{a} \cdot \nabla) \mathbf{b} + (\mathbf{b} \cdot \nabla) \mathbf{a}. \end{eqnarray}

I do not see where the curl $(\nabla \times)$ enter in this analysis. Can someone point out an example where if we do not add the curl terms we get different values on the left and on the right?

Answer 5

Gradient of a Dot Product Answer

The quantity $\overset{\rightarrow}\nabla\left( \overset{\rightarrow}A \bullet \overset{\rightarrow}B \right)$ is a vector quantity since $\overset{\rightarrow}\nabla$ is a vector operator on the vector scalar product $\overset{\rightarrow}A \bullet \overset{\rightarrow}B $. The answers that $\overset{\rightarrow}\nabla\left( \overset{\rightarrow}A \bullet \overset{\rightarrow}B \right)$ **is a scalar quantity are therefore incorrect.** For simplicity, cast $\overset{\rightarrow}A \bullet \overset{\rightarrow}B$ in Cartesian coordinates as: $\overset{\rightarrow}A \bullet \overset{\rightarrow}B= A_x*B_x+A_y*B_y+A_z*B_z$ and then from the [Scalar Chain Rule of Calculus (from Wolfram Math World][1]): $$\begin{aligned} \overset{\rightarrow}\nabla\left( \overset{\rightarrow}A \bullet \overset{\rightarrow}B \right) = \hat{x}\frac{\partial}{\partial x}\left(A_x*B_x+A_y*B_y+A_z*B_z\right) \\ +\hat{y}\frac{\partial}{\partial y}\left(A_x*B_x+A_y*B_y+A_z*B_z\right) \\ +\hat{z}\frac{\partial}{\partial z}\left(A_x*B_x+A_y*B_y+A_z*B_z\right) \\ =\hat{x}\left(\frac{\partial}{\partial x}A_x*B_x +\frac{\partial}{\partial x}A_y*B_y +\frac{\partial}{\partial x}A_z*B_z\right) \\ +\hat{y}\left(\frac{\partial}{\partial y}A_x*B_x +\frac{\partial}{\partial y}A_y*B_y +\frac{\partial}{\partial y}A_z*B_z\right) \\ +\hat{z}\left(\frac{\partial}{\partial z}A_x*B_x +\frac{\partial}{\partial z}A_y*B_y +\frac{\partial}{\partial z}A_z*B_z\right) \\ +\hat{x}\left(A_x*\frac{\partial}{\partial x}B_x +A_y*\frac{\partial}{\partial x}B_y +A_z*\frac{\partial}{\partial x}B_z\right) \\ +\hat{y}\left(A_x*\frac{\partial}{\partial y}B_x +A_y*\frac{\partial}{\partial y}B_y +A_z*\frac{\partial}{\partial y}B_z\right) \\ +\hat{z}\left(A_x*\frac{\partial}{\partial z}B_x +A_y*\frac{\partial}{\partial z}B_y +A_z*\frac{\partial}{\partial z}B_z\right) \\ \end{aligned} $$ Thus, $$ \overset{\rightarrow} \nabla \left( \overset{\rightarrow} A \bullet \overset{\rightarrow} B \right) = \left( \overset{\rightarrow}\nabla \overset{\rightarrow}A \right) \bullet \overset{\rightarrow}B + \left( \overset{\rightarrow}\nabla \overset{\rightarrow}B \right) \bullet \overset{\rightarrow}A $$ This result can be checked since: $$\overset{\rightarrow}\nabla= \hat{x}\frac{\partial}{\partial x}+ \hat{y}\frac{\partial}{\partial y}+ \hat{z}\frac{\partial}{\partial z} \text{ and }\\ \overset{\rightarrow}\nabla \overset{\rightarrow}A= \left( \hat{x}\frac{\partial}{\partial x}+ \hat{y}\frac{\partial}{\partial y}+ \hat{z}\frac{\partial}{\partial z} \right) \left( \hat{x}A_x+ \hat{y}A_y+ \hat{z}A_z \right) $$ Only the $\hat{x}$ terms on the right interact with $B_x$ and so forth for $\hat{y}$ with $B_y$ and $\hat{z}$ with $B_z$. The same for the left, that wherever there is $\frac{\partial}{\partial x}$ that there is also $\hat{x}$ in the result and so forth. So the result is correct.

I am hoping to provide additional updates

I am still working on additional updates. However, the current result shows two things clearly: 1) The result of $\overset{\rightarrow}\nabla \left(\overset{\rightarrow}A \bullet \overset{\rightarrow} B \right)$ is a vector quantity. And further it can be represented by vector operations (see page 147 in the quoted reference below for Gibbs Vector Analysis from Forgotten Books ).