What is the intuition behind calculation of the area of circle?

Question

I am learning about approximating the area of circle ($\pi r^2$) by the area of polygons ($\frac{1}{2}$ of number of sides * the distance between side and center * length of the side).

My question is about intuition: When the $n$ converges to infinity, we are getting a circle (polygon with an infinite number of sides with infinitely small lengths). How is the whole formula for polygon area converging to $\pi r^2$?

Can we calculate limit, using standard ways for working with limits? Thanks for the explanation and intuition.

Answer 1

You can use a bit of trigonometry to see this. The apothem (labeled $a$) in your diagram, is the adjacent side to the central angle $\phi = \frac{1}{2 n} (2 \pi) = \frac{\pi}{n}$ in a right triangle with hypotenuse $r$. The area of one of those right triangles is $\frac{1}{2} (r \sin \phi) (r \cos \phi) = \frac{1}{4} r^2 \sin (2 \phi)$. Since there are $2 n$ of these right triangles, the area of the inscribed regular polygon is

$$A_n = \frac{1}{2} n r^2 \sin (2 \phi) = \frac{1}{2} n r^2 \sin \left( \frac{2 \pi}{n} \right)$$

Taking the limit as $n$ approaches infinity, and keeping in mind that $\sin x \to x$ when $x \to 0$, we have

$$A_n \to \frac{1}{2} n r^2 \left( \frac{2 \pi}{n} \right) = \pi r^2$$

as desired.

Answer 2

Area of regular polygon $={1\over2}$ perimeter $\times$ apothem.

When the number of sides $n$ grows, the area of the polygon approaches the area of the circle, the perimeter of the polygon approaches the circumference of the circle, and the apothem of the polygon approaches the radius of the circle. Hence:

Area of circle $={1\over2}$ circumference $\times$ radius.

But we know by definition that

circumference $=2\pi\ \times$ radius

and substituting that into the previous formula we get the desired result:

Area of circle $=\pi$ $\times$ radius$^2$.

Answer 3

I am just gonna post because of the comment that OP doesn't want to know tools like $\sin$ or angles or radians I think as much as possible.

The $r^2$ dependency is easy too see by the definition of area as a limit of $\Delta x \Delta y$ (under suitable conditions) and if you know one upper/lower sum for a figure, scaling the sum is also such sum for the scaled figure.

Now, the definition of angle a point on unit circle extends could be in terms of length (needs a definition) of the arc extending from point $(0,1)$ to that point (thus angles lie in $[0,2\pi)$).

In particular $\pi$ makes sense as the angle the point $(-1,0)$ makes. Now given a sequence of polygons (the symmetric ones) whose vertices lie on the unit circle, we have to show that area is equal to the number $\pi$ defined above.

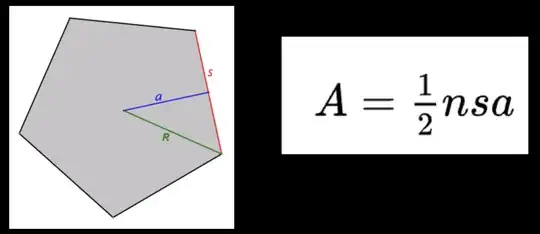
But for a $2N$-gon the area is $2N\cdot \sqrt{1-x^2}x$ where I am assuming the figure is divided into $2N$ many isosceles triangles of equal side $=1$, and the third side of lenght $2x$. In particular, the perimeter of the polygon is $2N\cdot 2x = 4Nx$.

Now the exact meaning of convergence of areas and perimeters at the same time in this case intuitively makes sense (but also there are fake proofs for why $\pi=4$ ) so I will assume that.

Now by definition $4Nx$ converges to $2\pi$ (double'ness is obvious from symmetry say) and $x\rightarrow0$ conditions gives area $=\pi$

Answer 4

As you add more and more sides to the polygon, the perimeter of all the polygon gets closer and closer to the perimeter of the circle, which is $2\pi r$.

Consider the triangles formed by connecting the ends of each side to the center. Using the polygon edge as the "base", as you add more and more edges, the height of each triangle gets closer and closer to r, as the angle at the center decreases.

The total area of the polygon gets closer and closer to the area of the circle, as the amount of leftover area decreases.

For n edges/triangles, this total area is $A = n(\frac{1}{2}bh) = \frac{bn}{2}h$.

We can make the above substitutions to see what the area converges to as n approaches infinity. $bn$ is perimeter of the polygon, which converges to $2\pi r$, and $h$ is the height of each triangle, which converges to $r$.

Substituting, we get $A = \frac{2\pi r}{2}r = \pi r^2$.