5

Now asked on MO here.

Define $f_1(z) = \cos(z)$, $f_{n+1}= \cos(f_n (z)) $, The question is Does $\lim\limits_{n \to \infty}f_n(z)$ exist for all $z \in \mathbb{C}$? And if the answer is no what is the sufficient conditions that $z$ should satisfy so that the limit exist? And what is the limit for such $z$?

We know that for real numbers $z\in \mathbb{R}$, the limit exists and is the solution to the equation $x=\cos(x)$. This result is well-established Here. However, the complex case seems more intricate due to the unbounded nature of the cosine function on $\mathbb{C}$ and the existence of infinitely many solutions to $\cos(z)=z$.

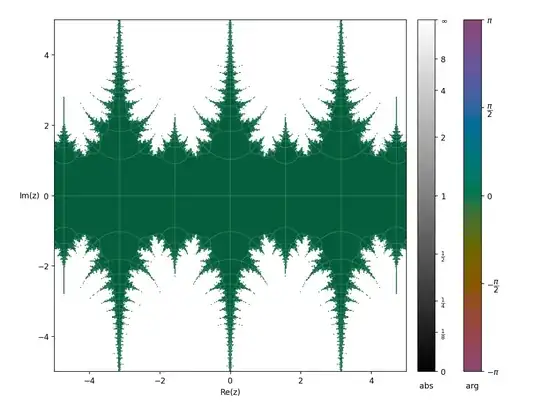
This is the graph of $f_{20}(z)$, it seems that if the limit exist then the limit is the real solution for $\cos(z)=z$, For some reason it seems that the other fixed points of $cos(z)$ doesn't "attract" the sequence of points, only the real solution do.

enter image description here

pie
  • 8,483
  • 3
    Apparently the Julia set of $\sin z$ is quite complicated, $\cos z$ is probably similar: https://paulbourke.net/fractals/sinjulia/, https://en.wikipedia.org/wiki/Julia_set – Qiaochu Yuan Jul 25 '24 at 02:59
  • For $z = 1+2i$ the sequence looks like this: $1+2i$ , $2.03272 - 3.0519 i$ , $-4.72475 + 9.44798 i$ , $78.3706 - 6340.75 i$, $-2.798836298519605\times 10^{2753} + 4.782822957668558\times 10^{2752} i$ so my guess is that the sequence doesn't converge. – jjagmath Jul 25 '24 at 18:28
  • I wonder if any results from iterated function systems exist that provide a test for this. – Andy Walls Jul 25 '24 at 18:31
  • @jjagmath The limit of $f_n$ is a fractal and it seems that it converge for some points – pie Jul 25 '24 at 19:33
  • 1
    Roughly speaking the $n$th solution of $\cos z = z$, $n > 1$, with positive real part is near $(2 \pi n, \log(4 \pi n))$ (see https://math.stackexchange.com/questions/4639887/show-that-cosz-z-has-a-solution-for-some-complex-number-z-non-real), where the derivative of $\cos$ has value $i (2 \pi n - \frac{1}{8 \pi n})$, which has modulus much larger than $1$. A similar claim applies for the solutions with negative real part, so only the real fixed point is attracting. – Travis Willse Jul 25 '24 at 20:39
  • Your first question was about the convergence for all $z\in\Bbb C$, so my comment was to observe that that was highly improbable. – jjagmath Jul 25 '24 at 22:23

0 Answers0