Where is the error in evaluating this integration:$$\int^{\infty}_{-\infty}\frac{\cos(2x)}{(1+x^2)^2}dx$$
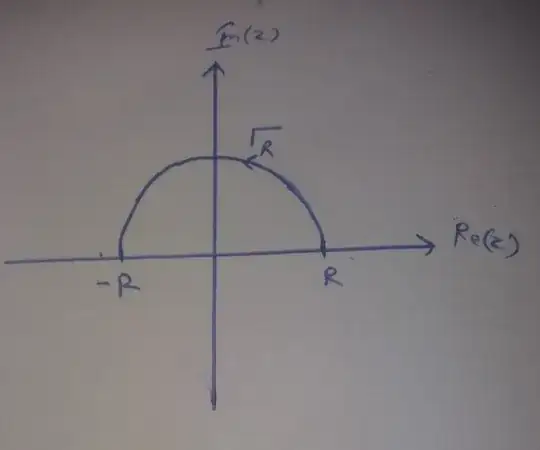
we have: $$\int_{C_R}\frac{\cos(2z)}{(1+z^2)^2}dz=\int_{-R}^{R}\frac{\cos(2x)}{(1+x^2)^2}dx+\int_{\Gamma_R}\frac{\cos(2z)}{(1+z^2)^2}dz=2i\pi\text{Res}(f(z),z=i)=\frac{\pi(3-e^4)}{2e^2}$$
and we have : $$0\le | \int_{\Gamma_R}\frac{\cos(2z)}{(1+z^2)^2}dz | \le \frac{\pi R}{(R^2-1)^2}$$ Let $$R\to \infty $$ this implies that :$$\int_{\Gamma_R}\frac{\cos(2z)}{(1+z^2)^2}dz=0$$
therfore: $$\int_{-\infty}^{\infty}\frac{\cos(2x)}{(1+x^2)^2}dx=\frac{\pi(3-e^4)}{2e^2}$$ but this is result is wrong Because using wolfram alpha : $$\int_{-\infty}^{\infty}\frac{\cos(2x)}{(1+x^2)^2}dx=\frac{3\pi}{2e^2}$$