Relationship of the Egg Riddle solution to bisection and $\log(N)$ function?

Question

I stumbled upon the video "Can you solve the egg drop riddle? - Yossi Elran" on the TED-Ed YouTube channel.

What I found interesting is that in the solution, given that the triangle numbers grow quadratically, it means that in this kind of search, given $N$ floors, one needs about $\sqrt{N}$ drops in general to find the right floor.

Then, comparing this to good old bisection: If there were an infinite number of test eggs, the solution would have been to bisect the range, so order of $\log N$ drops in general to find the right floor.

Trying to bridge between two eggs, and infinite number of eggs:

My intuition tells me that if there were three eggs, this would result in tetrahedral numbers? So one would need about $\sqrt[3]{N}$ steps in general to find the right floor (as the number $N$ of floors grows)?

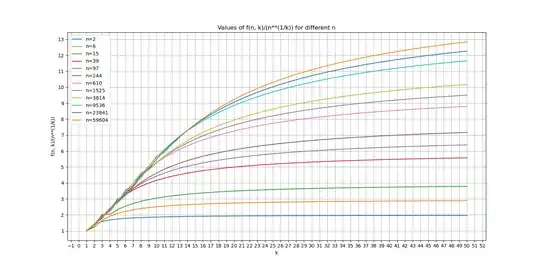
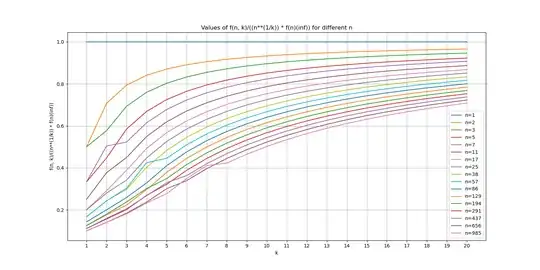
Taking this intuition further: four eggs should mean growth of pentatope numbers, five eggs $5$-simplex numbers, and so on... for $K$ eggs resulting in $N$ to the $K$ rising factorial divided by $K$ factorial.

Logic says that as $K$ is unlimited (i.e. $K=N$, there are as many eggs as there are floors), and as $K=N$ tends to infinity, the inverse of this function should tend to $\log(N)$ to reach the limit that bisection has with unlimited number of eggs.. but I'm not sure how to get that. I got into $\lim_{N\to \infty} \sqrt[N]{N}$ type of situation, which tends to $1$ instead.

Anyone know if there is a proof that bridges the finite number of eggs ($\sqrt[K]{N}$) to infinite number of eggs ($\log N$) as $N$ tends to infinity?

It's generally discouraged to have a problem statement which is embedded within a video source. Moreover, it looks like the problem here is the same as the one found here, which includes a short verbal statement of the question. So I'd suggest including the textual version first-and-foremost, and provide the video link as further context. — Semiclassical, Jul 04 '24 at 21:49
See https://stackoverflow.com/questions/11603218/three-egg-problem and the links there. Also, https://stackoverflow.com/questions/40118972/understanding-egg-drop-algorithm-for-more-than-two-eggs and https://stackoverflow.com/questions/48763516/egg-dropping-puzzle-suggestion-needed and https://stackoverflow.com/questions/51737262/recursion-in-egg-drop-puzzle — Gerry Myerson, Jul 07 '24 at 09:48
Also https://math.stackexchange.com/questions/2012591/eggs-and-floors-puzzle-extended-generalized and dozens of other websites. — Gerry Myerson, Jul 07 '24 at 09:54
Yes, I did read them (already before posting), though none of them address the question that I posted, namely how the log(N) would come into play in the limit. Thanks for posting them nevertheless! — trojj, Jul 09 '24 at 18:43

score 2 · Answer 1 · answered Jul 07 '24 at 07:59

Defining the function of minimum number of drops required with $k$ eggs for $n$ floors:$$f(n, k) = \begin{cases} 0 & \text{ if } n=0\\ \infty & \text{ otherwise if } k=0 \\ \min\limits_{x=1}^{x=n}\bigg(1 + \max\big(f(x-1, k-1), f(n-x, k)\big)\bigg) & \text{otherwise} \end{cases}$$

As you said, for any particular $k_0$, $f(n, k_0) \in \Theta(n^{1/k})$. But for a fixed $n_0$, $f(n_0, k)$ drops very fast to $\lfloor \log_2 (n_0 + 1) \rfloor$ at just $k = \lfloor \log_2 (n_0 + 1) \rfloor$, and then remains constant.

I've drawn some plots to show how this drop occurs

First two plots of $\frac{f(n_0, k)}{n_0^{1/k}}$ for some select $n_0$'s
Second two plots of $\frac{f(n_0, k)}{n_0^{1/k}\lfloor \log_2 (n_0 + 1) \rfloor}$ for some select $n_0$'s

Below is my code to draw these plots, feel free to use it to gain more insights.

import math
import matplotlib.pyplot as plt
N, K = map(int, input().split())
dp = [[N+1 for _ in range(K+1)] for _ in range(N+1)]
for k in range(K+1):
    dp[0][k] = 0
for k in range(1, K+1):
    x = 1
    for n in range(1, N+1):
        while x <= n:
            newVal = 1 + max(dp[x-1][k-1], dp[n-x][k])
            if newVal <= dp[n][k]:
                dp[n][k] = newVal
                x += 1
            else:
                break
        x -= 1
fig, ax = plt.subplots()
for n in [math.floor(2.5i) for i in range(1, 100) if math.floor(2.5i) <= N]:
    ax.plot([k for k in range(1, K+1)],
            [dp[n][k] / ((n ** (1/k)) * dp[n][K]) for k in range(1, K+1)],
            label=f'n={n}')
ax.legend(loc='lower right')
ax.set(xlabel='k', ylabel='f(n, k)/((n(1/k)) * f(n)(inf))',
       title='Values of f(n, k)/((n(1/k)) * f(n)(inf)) for different n')
ax.grid()
plt.gca().xaxis.set_major_locator(plt.MultipleLocator(1))
plt.gca().yaxis.set_major_locator(plt.MultipleLocator(1))
plt.show()

Thanks for this great insight. If I interpret the graphs correctly, they indeed look like to confirm the intuition that k eggs has the order of O(pow(n, 1/k)), and the number of steps converges to log(N). — trojj, Jul 09 '24 at 18:45

Relationship of the Egg Riddle solution to bisection and $\log(N)$ function?

1 Answers1