Given a multigraph $G$ embedded in the plane call a maximal set of parallel edges between $u,v$ such that only one of the induced faces (a face is a connected region of $\mathbb{R}^2 \backslash G $) contains nodes besides $u$ or $v$ a topologically parallel set (tell me if there is standard terminology for this).
Given a topologically parallel set $S$ of edges between $u$ and $v$ we say that an edge $e$ dipsinto the set $S$ if $e$ intersects some but not all edges of $S$.
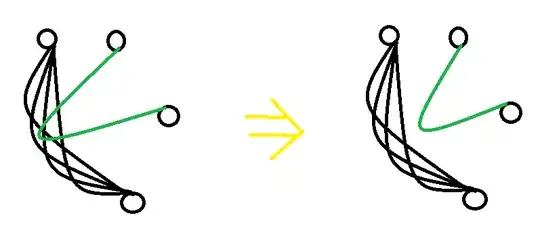 $\phi $ into $\phi'$" />
$\phi $ into $\phi'$" />
Is it true that Given a multigraph $G$ with an embedding $\phi$, there is an embedding $\phi'$ with $\phi(V) = \phi'(V)$, preserving the topologically parallel sets such that no edge $e$ dips into a topologically parallel set. Further if two edges cross in $\phi'$, then they cross in $\phi$.
I'm fairly sure this is true simply perturb the drawing so that edges no longer dip into topologcially parallel sets.