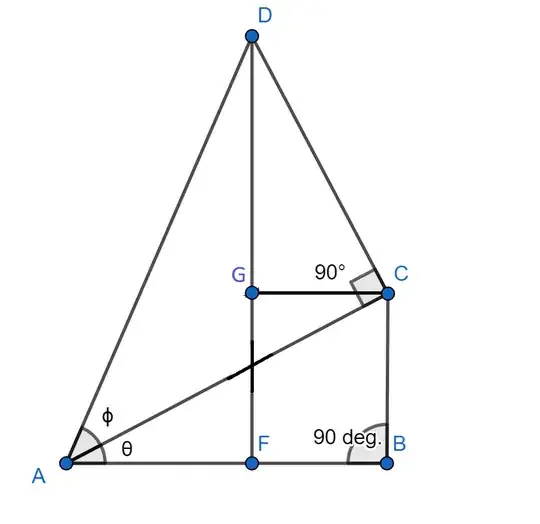
I'm doing a refresher on high school math and wanted to prove the $\sin(\theta + \phi) = \sin(\theta)\cos(\phi)+\cos(\theta)\sin(\phi)$ identity but I can't get it right.
I drew two right triangles $ACD$ and $ABC$ on on top of another like can be seen in this picture:
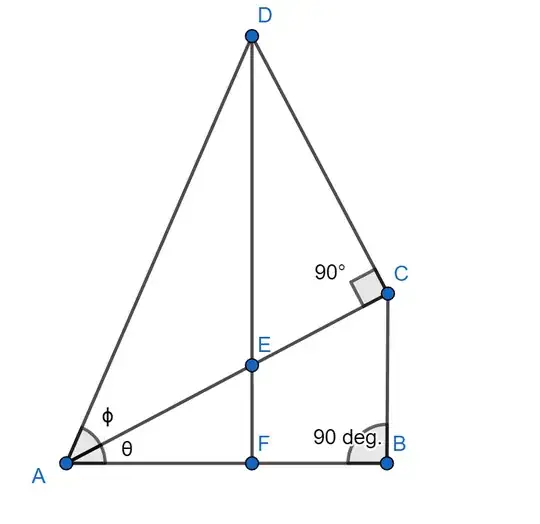 Let's assume that $\overline{AD}=1$ for simplicity.
Also $DF$ is perpendicular to $AB$.
Then $\sin(\theta+\phi)=\overline{DF} = \overline{FE}+\overline{DE}$. Notice that
$\angle{DEC}=\angle{AEF}= \pi/2 - \theta$.
Thus $\overline{DE}=\overline{DC}/\sin(\angle{DEC})=\sin(\phi)/\cos(\theta)$.
Let's assume that $\overline{AD}=1$ for simplicity.
Also $DF$ is perpendicular to $AB$.
Then $\sin(\theta+\phi)=\overline{DF} = \overline{FE}+\overline{DE}$. Notice that
$\angle{DEC}=\angle{AEF}= \pi/2 - \theta$.
Thus $\overline{DE}=\overline{DC}/\sin(\angle{DEC})=\sin(\phi)/\cos(\theta)$.
Note that $\cos(\phi)=\overline{AC}$ and that $\overline{EC}=\overline{DE}\cos(\angle{DEC})=\overline{DE}\sin(\theta)$. From this we get $\overline{AE}=\overline{AC}-\overline{EC}=\cos(\phi) - \overline{DE}\sin(\theta) = \cos(\phi)-\sin(\phi)\tan(\theta)$. From this $\overline{FE}$ can be calculated as $\overline{AE}\sin(\theta)=\cos(\phi)\sin(\theta)-\sin(\phi)\tan(\theta)\sin(\theta)$. So finally, $$\sin(\theta+\phi)=\overline{DF}=\overline{FE}+\overline{DE}=\cos(\phi)\sin(\theta)-\sin(\phi)\tan(\theta)\sin(\theta)+\sin(\phi)/\cos(\theta),$$ which is not the correct relation.
Even though I double checked the steps, I can't find an error in my work. I'd be thankful for pointing out what went wrong here.