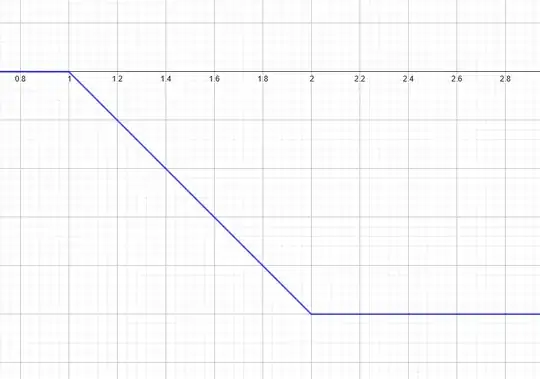
I am dealing with a piecewise affine function $f$ defined as follows: $f(x)=0$ if $x<1$, $f(x)=1-x$ if $x\in [1,2]$ and $f(x)=-1$ otherwise.
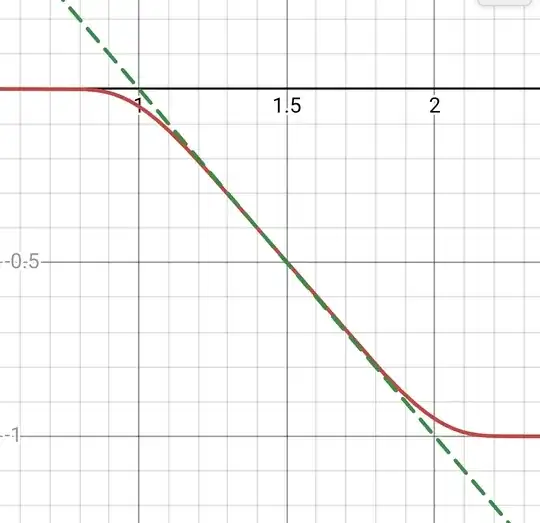
 I want to make it smooth. I looked at sigmoid functions of the form:
$$
g_{a,b}(x)=\frac{1}{1+e^{-a(x-b)}},
$$
but I think that these functions are useful only when dealing with indicator functions. I thought of adding a circle arc to make smooth the corners:
I want to make it smooth. I looked at sigmoid functions of the form:
$$
g_{a,b}(x)=\frac{1}{1+e^{-a(x-b)}},
$$
but I think that these functions are useful only when dealing with indicator functions. I thought of adding a circle arc to make smooth the corners:
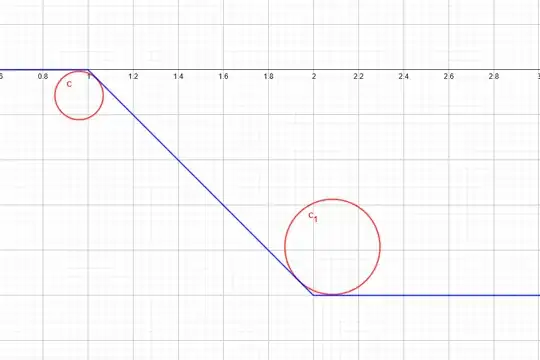
But I am stuck on how to parametrize them so I get a smooth function $g_{\epsilon}$ that converges to $f$ when $\epsilon$ goes to zero.