Approximating the length of a circular arc using geometrical construction. How does it work?

Question

I was going through my Engineering Drawing textbook and came upon this topic. Using only a compass and a straightedge, one can supposedly approximate the length of a given circular arc by following the steps below.

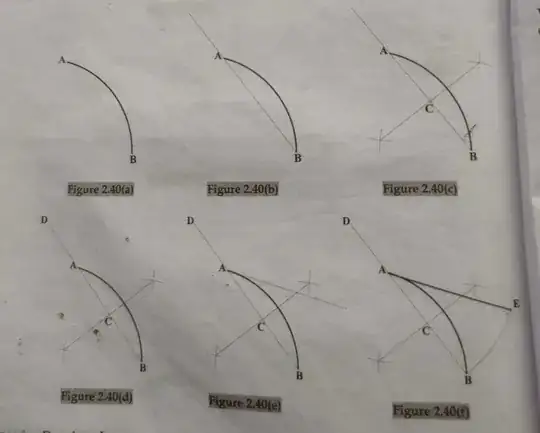
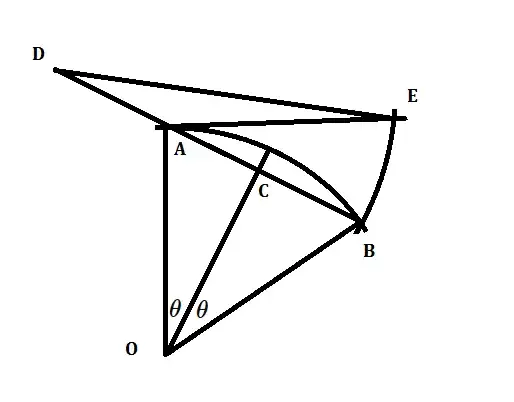
1. Let AB be the given circular arc.
2. Draw chord AB and extend it to one side.
3. Draw perpendicular bisector of AB to get its midpoint C.
4. Mark point D on the extended chord such that AC=AD.
5. Draw a tangent line to the given arc passing through point A.
6. With D as center and DB as radius, draw an arc which intersects the tangent line passing through A at point E.

We get AE which is the required arc length.

Here is a picture from the book demonstrating the above steps.

My question is how does this approximation work?

Before this topic, there was a section on approximating the circumference of a circle using a compass and straightedge only. Using basic trigonometry, I realized it was using the relation

$\ 2π \approx \sqrt{6^2+ (1+\sin(60 ^{\circ}))^2}$

to construct a right angled triangle whose hypotenuse would approximate the circumference of the circle utilizing above approximation, which I found pretty impressive.

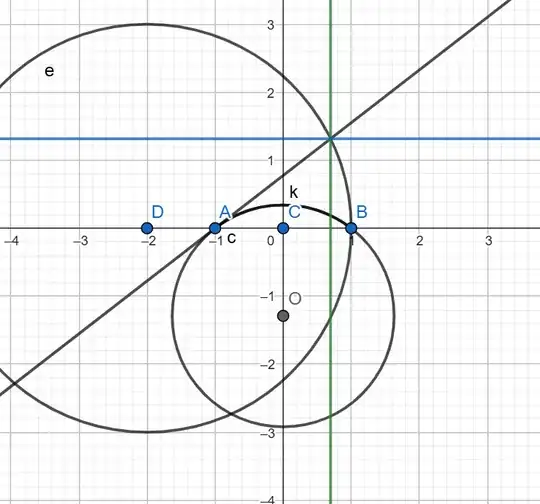
But, when I tried to find out how the method worked for approximating the arc length of a circular arc, I had no luck. I tried some preliminary angle chasing and later tried using coordinate geometry but couldn't come up with an expression for length of AE.

How could I show that the above steps work for approximating arc length?

Answer 1

Here is the total construction :

Let the angle made by the arc $AB$ be $2\theta$
Let Circle radius be $1$ (We can always scale it up later)
Let $AC=BC=AD=r$

We can see that $\angle AOC = \theta$
$\sin \theta = r$
$\angle EAB = \theta$

$DB=DE=3r$
$\angle DAE = \pi - \theta$

Using law of Cosines with triangle $DAE$ :
$DE^2 = DA^2+AE^2-2(DA)(AE)\cos(\pi-\theta)$
$(3r)^2 = (r)^2+(P)^2+2(r)(P)\cos(\theta)$
$0 = +(P)^2+2(r)(P)\cos(\theta)-8(r)^2$

Solve that Quadratic Equation :
$P = r [ \pm \sqrt{\cos^2(\theta)+8}-\cos(\theta) ]$
We can see that the $\pm$ in the Solution is $+$ , to avoid negative lengths.

$P = r [ \sqrt{1-\sin^2(\theta)+8}-\sqrt{1-\sin^2(\theta)} ]$

$P = AE = \sin(\theta) [ \sqrt{9-\sin^2(\theta)}-\sqrt{1-\sin^2(\theta)} ]$

Checking with Wolfram , I get :

$P = AE = 2\theta-O(\theta^5)$

[[ Alternately , we can use $\sin \theta \approx \theta$ & $\sin^2 \theta \approx 0$ when $\theta$ is close to $0$ : We will get $P = AE \approx \theta [ \sqrt{9-0}-\sqrt{1-0} ] \approx 2\theta$ , without Series Expansion ]]

We know Arc length $\overline{AB} = 2\theta$

$AE \approx 2\theta$

Hence the method works to generate the Approximation to the arc length.

Answer 2

Prem had attempted this problem and posted their work here earlier & a while later too. I've tried to correct and continue their work.

Let the angle made by the arc $AB$ be $2 \theta$.
Let radius of circle be $R$.
Let $A C=B C=A D=r$ and let $AE =P$.

We can see that $\angle A O C=\theta$ $$ \begin{aligned} & R\sin \theta=r \\ & \angle E A B=\theta \\ & D B=D E=3 r \\ & \angle D A E=\pi-\theta \end{aligned} $$

Using law of Cosines with triangle $D A E$ : $$ \begin{aligned} & D E^2=D A^2+A E^2-2(D A)(A E) \cos \\ & (\pi-\theta) \\ & (3 r)^2=(r)^2+(P)^2+2(r)(P) \cos (\theta) \\ & 0=+(P)^2+2(r)(P) \cos (\theta)-8(r)^2 \end{aligned} $$

Solve that Quadratic Equation : $$ P=r\left[ \pm \sqrt{\cos ^2(\theta)+8}-\cos (\theta)\right] $$

We can see that the $\pm$ in the Solution is + , to avoid negative lengths. $$ \begin{aligned} P=R\sin\theta\left[ \sqrt{\cos ^2(\theta)+8}-\cos (\theta)\right] \end{aligned} $$ Now, we have Arc length \begin{aligned} \overline{A B}=R×2\theta \end{aligned} So, the approximation must be \begin{aligned} 2\theta \approx \sin\theta\left[ \sqrt{\cos ^2(\theta)+8}-\cos (\theta)\right] \end{aligned} And, sure enough, the Taylor series expansion for the expression on the right is \begin{aligned} 2\theta - \frac{4{\theta}^5}{135}-\frac{4\theta^7}{1701}+\frac{4\theta^9}{10935}+... \end{aligned}

\begin{aligned} Q.E.D\end{aligned}

Wow, with all this going on behind a simple geometrical algorithm, I wonder if there's a more intuitive approach to arriving at this approximation. Always open to more answers. Thank you.

Answer 3

Without loss of generality, fix $A,B$ on the $x$-axis at $(-1,0)$ and $(1,0)$ respectively. Let the center of the circle containing the arc $AB$ be $O=(0,t)$ fixed on the $y$ axis, which has $t\le0$ parameterizing the system. Hence also $C$ is the origin and $D=(-2,0)$.

Observe that angle $\angle COB=\arctan(1/|t|)$, subtending half of the arc $AB$, so that the arc $AB$ has length $2\angle COB\cdot \overline{OB}=2\arctan(1/|t|)\sqrt{1+t^2}$. Observe also that the line $OA$ has slope $t$, such that the tangent to the arc at $A$, perpendicular to $OA$, has slope $-1/t$. The circle constructed in the problem statement with center $D$, which is now fixed with radius $\overline{DB}=3$, is intersected at point $E$ by the tangent at $A$, which must be at $\sqrt{3^2-(x-(-2))^2}=-1/t(x-(-1))$, which in turn can be solved for $E_x$, the horizontal component of $E$. The segment $AE$, which gives the desired approximation, therefore has length $\sqrt{(\overline{AC}+E_x)^2+E_y^2}=\left(E_{x}+1\right)\sqrt{1+\frac{1}{t^{2}}}$. This simplifies to $\overline{AE}=\dfrac{t+\sqrt{8+9t^{2}}}{\sqrt{t^{2}+1}}$.

We now aim show that $\overline{AE}=F(t)$ approximates arc $AB=f(t)$. Consider for $t\to-\infty$ the asymptotics, $\sqrt{8+9t^{2}}\sim -3t\left(1-\frac{4}{9t^{2}}\right)$ and $\arctan\left(\frac{1}{t}\right)\sim 1/t$. This gives $$\frac{F(t)}{f(t)}=\frac{\frac1{\sqrt{t^{2}+1}}\left({t+\sqrt{8+9t^{2}}}\right)}{-2\arctan\left(\frac{1}{t}\right)\sqrt{1+t^{2}}}\sim\frac{3t^{2}-2}{3\left(1+t^{2}\right)} \\$$

Therefore, $F(t)\sim \left(1-\frac{5}{3t^{2}}\right)\,f(t)$. That is, $\overline{AE}$ makes a good approximation to the arc $AB$, which is asymptotically exact for arcs of small curvature.

Answer 4

Starting from @Prem's good answer, if we want to solve for $\theta$ the equation

$$q=\frac P R=\sin(\theta)\Big(\sqrt{\cos ^2(\theta)+8}-\cos (\theta)\Big)$$ let $\theta=\cos ^{-1}(x)$. This gives $$q=\sqrt{1-x^2}\left(\sqrt{x^2+8}-x\right)$$ Squaring and assuming $x\neq 0$, this reduces to the cubic equation $$2 q^2 x^3+q^4 x^2+8 q^2x+16=0$$ which can be solved with radicals.

The discriminant being $$\Delta=512 q^4 \left(q^4-54\right)$$ there is only one real root as long as $q \lt \sqrt{ 3 \sqrt{6} }=2.71081$. Using the hyperbolic solution for $x$ and back to $\theta$, for this range

$$\large\color{blue}{\theta=\cos^{-1}\left(\sqrt{\frac{32-q^2\sqrt{9-q^2}-3 q^2}{2 q^2+32}}\right)}$$ We have all what is required with no approximation.

Edit

If we had done the series expansion for small $\theta$ and then used power series reversion, we could have obtained $$\theta=\frac{q}{2}+\frac{q^5}{2160}+\frac{q^7} {108864}+\frac{q^9}{559872}+O\left(q^{11}\right)$$ which is exactly the series expansion of the "blue" formula.