1

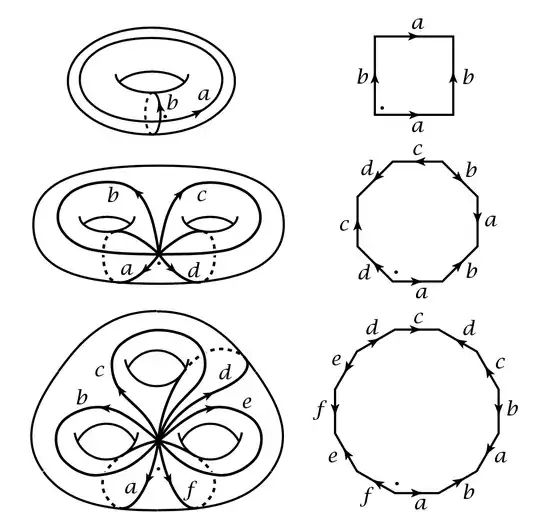
I'm wondering if there is a way to 'unfold' higher genus surfaces in the way that a torus can be unfolded into a square after making two cuts to the torus, one around the perimeter of the hole and another that intersects the first cut perpendicularly.

If so, what is the resultant shape? And what sort of transformation occurs to points on the surface as the surface is 'unfolded'.

Also, when a sphere is mapped to a circle on the coordinate plane, the boundary of the circle corresponds to a single point at the pole opposite the point on the sphere mapped to the center of the circle. Since spheres are genus 0 objects, is that boundary circle analogous to the borders of the square that a torus is mapped to?

An answer to a previous version of this question showed me that you can generalize upward from a g1 surface, but can you generalize downward to g0?

--

This question has been edited to match the answer originally posted, which states that surfaces with genus > 0 can be 'unfolded' to n-gons where the number of sides = 4g, with g the genus of the surface.

Rich Jensen
  • 697
  • What do you mean by "assigning coordinates"? What do you expect the coordinate functions to behave like? – tomasz May 01 '24 at 19:25
  • @tomasz The coordinate function should be able to identify any point on the surface, with ambiguity restricted to a definable subset of points. For example, if you map the points on a torus to a square section of the plane bounded by $(0,0)$ & $(1,1)$, only coordinates on the boundary would be ambiguous (e.g. $(n,1)=(n,0)$, $(1,n)=(0,n)$), if that makes sense. – Rich Jensen May 01 '24 at 19:59
  • @tomasz, with a sphere mapped to a circle of radius $r$, then ambiguity would exist only with coordinates $(r,\theta)$, where every point of this form would refer to the point on the sphere opposite the point $(0,0)$ – Rich Jensen May 01 '24 at 20:04
  • 3
    This question is totally unclear. My suggestions is to read introductory material on smooth manifolds in any textbook on differential topology. – Moishe Kohan May 01 '24 at 21:42
  • 1
    @RichJensen: Any (second-countable) manifold can be "parametrised" this way, since there is a bijection with $[0,1]$. – tomasz May 01 '24 at 23:22
  • 2
    What you're groping for is the definition of an atlas of coordinate charts for manifold, such as you'll learn in a book or course on differential topology. As you'll see if you put in some time learning that subject, any higher genus surface, or any manifold, is covered by the union of some number of coordinate charts. Each individual chart is "nonsingular" in a certain way. As you seem aware of in the case of the sphere, it is very rare that one single such chart will cover the whole manifold. – Lee Mosher May 02 '24 at 01:08
  • @MoisheKohan If I knew enough to ask the question clearly, I probably wouldn't have needed to ask the question at all. If I knew where to find the answer to the question, I definitely wouldn't have needed to ask it here. :) – Rich Jensen May 02 '24 at 18:08
  • Then the right thing to do is ask for references. There are many suggestions that can be found for instance here. – Moishe Kohan May 02 '24 at 18:19
  • @LeeMosher Can you write up this comment as an answer? I didn't realize that applying a coordinate system would be different from the relationship between a genus $g$ surface and a $4g$-gon, because, well, I didn't even know such a relationship existed! – Rich Jensen May 02 '24 at 18:53
  • The trouble is that turning my comment into an answer would be tantamount to writing a chapter in a textbook on differential topology. I'm in agreement with @MoisheKohan on this point: as written your question is too vague, but an appropriately written question asking for references would more-or-less be a duplicate. – Lee Mosher May 02 '24 at 19:28
  • @LeeMosher, Honestly, I think your comment would work well as an answer pretty much as is. You give the technical term for what I'm looking for, provide a description of it that is suitable for a 'general reader', and point me in the right direction for more info. An example of a manifold that requires more than one chart would be a sort of cherry on top, hardly necessary, but a nice bonus. – Rich Jensen May 02 '24 at 19:41
  • See https://mathoverflow.net/questions/120799/manifolds-admitting-cw-structure-with-single-n-cell for a related but more general question – ronno May 09 '24 at 07:14

1 Answers1

2

While your question is a bit imprecise (which is fine!), the answer is more or less yes. The idea is to generalize the "coordinates" on the torus given by the unit square. Here is a picture from Hatcher's Algebraic Topology which describes the idea:

enter image description here

For example, consider the genus two surface pictured in the middle row. The "coordinates" on this surface are given by an octagon, with the "ambiguity" given by identifying pairs of edges as prescribed in the above diagram (e.g., the two edges labeled $a$ are identified by matching the arrows). It's a bit tricky to see how this gives you a genus two surface, but it is a worthwhile exercise. There are several posts on this website that provide a thorough explanation if you get stuck.

In general, a genus $g$ surface is given by identifying pairs of edges in a $4g$-gon. The precise statement is that, if $S$ is a surface of genus $g$ and $P \subseteq \mathbb{R}^2$ is a $4g$-gon, there is a quotient map (in the sense of topology) from $P$ to $S$. Note that the word "coordinates" is usually reserved for a slightly different (though certainly related!) notion in differential geometry/topology. It is a bit better (though still imprecise) to call the quotient map $P \to S$ a parametrization of the surface $S$.

Frank
  • 3,359
  • "It's a bit tricky to see how this gives you a genus two surface, but it is a worthwhile exercise." -- I can kind of visualize distorting the octagon to get there, but please don't ask me to do that with the genus three surface! – Rich Jensen May 02 '24 at 18:41
  • One other note... The $4g$ polygon relationship seems to make sense, using this logic: With a torus, two sides of the square correspond to a 'seam' along the hole in the torus, and the other two sides correspond to a 'cut' which does not turn the manifold into two disconnected surfaces. Thus, a genus 2 surface would have one more hole (= two more sides to the polygon) and allow one more cut (= two more sides). Is this a roughly accurate understanding of what's going on here? – Rich Jensen May 02 '24 at 18:57
  • 1
    @RichJensen Yup! That’s the rough idea. – Frank May 03 '24 at 02:08
  • MSE closed the question, but I thought your answer was great, so I edited it to have it reopened. I added a question about going from g1 to g0, I think I've got the idea for going up in hand, but what's going on with turning a sphere into a circle? Is there a way of visualizing the boundary of the circle in terms of the n-gons with directed sides? Or is the sphere/g0 kind of its own little weird thing? – Rich Jensen May 20 '24 at 19:23