Posted on MO since it is unanswered in MSE
It is known that the number of real roots of a random polynomial with real coefficients is much smaller than the number of complex roots. WLOG, assume that the coefficients are uniformly random in $(-1,1)$ for if not then we can divide each coefficient by the coefficient with the largest absolutely value to scale each coefficient to $(-1,1)$. Then the number of real roots of a polynomial of degree $n$ is asymptotic to $\displaystyle \frac{2\log n}{\pi} + o(1)$. Similar asymptotics hold for other distribution of the coefficients however for the rest of this post we assume that the coefficients are uniformly random in $(-1,1)$. This means that the number of complex roots is approximately $\displaystyle n - \frac{2\log n}{\pi}$.
Definition 1: The largest root of a polynomial is the root with the largest modulus. Definition 2: The smallest root of a polynomial is the root with the smallest modulus.
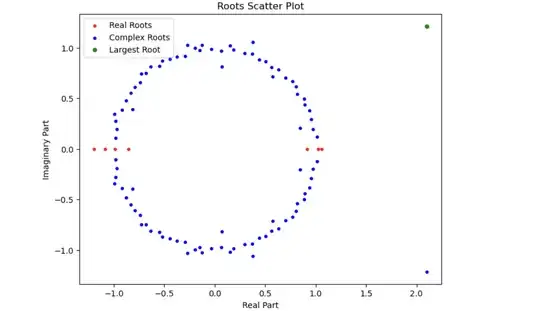
The above graph shows the roots of a polynomial of degree $101$; the largest root is in the top right corner in green.
Is the largest or the smallest root more likely to be complex or real? The naive guess is that the largest or the smallest root is more likely to be complex than real because there are exponentially more complex roots than real roots as seen from the above asymptotic.
However, experimental data shows that
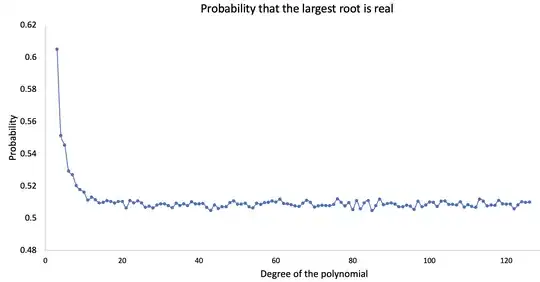
- Probability that the largest root is real is equal to the probability that the smallest root is real and this probability is greater than that of either of them being complex.
- This probability decreases to $1/2$ as $n \to \infty$ as shown in the above graph (created using a Monte Carlo simulation with $10^5$ trails for each value of $n$).
- Note: Instead of uniform distribution, if we assume that the coefficients are normally distributed with mean $0$ and standard deviation $1$ and scaled to $(-1,1)$, the above observation and limiting probabilities hold.
It is counter intuitive that despite being much exponentially fewer in number, real roots are more likely to contain the largest as well as the smallest roots. In this sense, the largest as well as the smallest roots is biased towards reals.
Question 1: What is the reason for this bias?
Question 2: Does the probability that the largest (or the smallest) root of a polynomial of degree $n$ is real approach $\frac{1}{2}$ as $n \to \infty$?
Update 2-May-2024: We can quantify the observed bias as follows. Let $P(L|R)$ be the probability that a root is the largest given that it is real and let $P(L|C)$ be the probability that a root is the largest given that it is complex. Similarly, let $P(S|R)$ be the probability that a root is the smallest given that it is real and let $P(S|C)$ be the probability that a root is the smallest given that it is complex. Then the experimental data says that
$$ P(L|R) = P(S|R) \approx \frac{\pi}{4\log n}, $$
$$ P(L|C) = P(S|C) \approx \frac{\pi}{2n\pi - 4\log n}. $$