Draw tangents at 3 random points on a circle to form a triangle. Show that the probability that a random side is shorter than the diameter is $1/2$.

Question

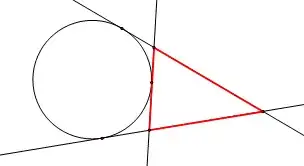
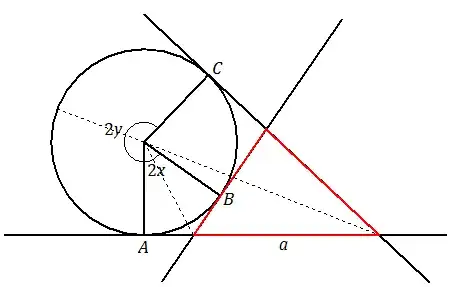
Choose three uniformly random points on a circle, and draw tangents to the circle at those points to form a triangle. (The triangle may or may not contain the circle.) For example:

What is the probability, $P$, that a randomly chosen side of the triangle is shorter than the diameter of the circle?

I have found that $P=\frac12$ by using integration, and I will post my answer below. But since the probability is so simple, I am looking for an intuitive explanation.

(Having said that, a probability's simplicity is no guarantee that there is an intuitive explanation; for example here and here are probability questions that have answers of $1/2$ but have resisted intuitive explanations.)

Edit: If two or more of the tangent lines are parallel or coincident, re-choose the three points.

Answer 1

Here is my non-intuitive answer.

Assume the circle is $x^2+y^2=1$, and the points are:
$A\space(\cos(-\alpha), \sin(-\alpha))$ where $0<\alpha<2\pi$
$B\space(\cos \beta, \sin \beta)$ where $0<\beta<2\pi$
$C\space(1,0)$

The tangent at $A$ has equation $y=(\cot\alpha)(x-\cos\alpha)-\sin\alpha$.
The tangent at $B$ has equation $y=-(\cot\beta)(x-\cos\beta)+\sin\beta$.
The tangent at $C$ has equation $x=1$.

Assume the chosen side is the one through $C$. This side has length $|(\cot\alpha)(1-\cos\alpha)-\sin\alpha+(\cot\beta)(1-\cos\beta)-\sin\beta|$, so the probability $P$ is

$$P(|(\cot\alpha)(1-\cos\alpha)-\sin\alpha+(\cot\beta)(1-\cos\beta)-\sin\beta|<2).$$

Let $\alpha=Y-X$ and $\beta=Y+X$. Using basic trigonometric identities, and symmetry, $P$ simplifies to

$$P\left(Y<\arccos\left(\frac{-\cos X+\sqrt{1+\sin^2 X}}{2}\right)\right)$$

where $0<X<\pi$, and $0<Y<\frac{\pi}{2}$.

So we have

$$P=\frac{2}{\pi^2}\int_0^\pi f(X)dX$$

where $f(X)=\arccos\left(\frac{-\cos X+\sqrt{1+\sin^2X}}{2}\right)dX$.

Now let $g(X)=f\left(X+\frac{\pi}{2}\right)-\frac{\pi}{4}$.

$$P=\frac{2}{\pi^2}\left(\int_{-\pi/2}^{\pi/2}g(X)dX+\frac{\pi^2}{4}\right)$$

$\sin (g(X)+g(-X))$ simplifies to $0$, so $-g(-X)=g(X)$, so $g(X)$ is an odd function.

$$\therefore P=\frac12$$

Answer 2

Here is an extended comment: There is a geometric equivalence to an earlier question of yours, also a geometric probability question wherein the answer of $\frac 12$ resists explanation.

Claim. Let $ABC$ be a triangle inscribed in the unit circle, and let $E$ and $F$ be the intersections of the tangents at $A$ and $C$ and at $B$ and $C$, respectively. Let $A'$ be the point diametrically opposite $BC$. Then $$EF>2\text{ if and only if } BC>A'B\cdot A'C.$$ Proof. Represent $A$, $B$, and $C$ by complex numbers $a$, $b$, and $c$, so that $A'=-a$, $E=\frac{2ac}{a+c}$, and $F=\frac{2ab}{a+b}$. Then \begin{align*} \frac{EF}2=\frac12\left|\frac{2ac}{a+c}-\frac{2ab}{a+b}\right| &=\left|\frac c{a+c}-\frac b{a+b}\right|\\ &=\left|\frac a{a+b}-\frac a{a+c}\right|=\left|\frac{b-c}{(a+b)(a+c)}\right|=\frac{BC}{A'B\cdot A'C}.\ \ \square\end{align*} (There should also be a geometric or trigonometric proof, but I think the complex proof is rather clean.)

If $A$, $B$, and $C$ are chosen uniformly at random on the unit circle, then the distribution of $\triangle A'BC$ is the same as that of $\triangle ABC$. So, the probability that $EF>2$ is equal to the probability that $BC>AB\cdot AC$. The earlier question of yours is exactly the observation that this second probability equals $\frac12$.

Answer 3

Assume the radius of the circle is $1$. Call the three random points $A,B,C$. Point $A$ is the lowest point on the circle. The arc from $A$ to $B$ measured anticlockwise has length $2x$, and the arc from $A$ to $C$ measured clockwise, where $0<x<\pi$ and $0<y<\pi$.

Assume that the randomly chosen side (or the line that it is coincident with) goes through $A$. Call the length of this side $a$.

$$P(a<2)=P(|\tan x+\tan y|<2)=P\left(\left|\frac{\tan x+\tan y}{2}\right|<1\right)$$

Since $\tan x$ and $\tan y$ are independent random variables with the standard Cauchy distribution, their average also has the standard Cauchy distribution, so it follows immediately that the probability is $\frac12$.

Remarks

I got this idea from an answer to a related question. (As @Carl Schildkraut has shown, these two questions are geometrically equivalent.)

I would still be interested in a proof from pure geometry, like this answer to that related question.

Answer 4

Let $T_1,T_2,T_3$ be the tangent points so that $A,T_1,B$ colinear. $$P(AT_1\leq r)=\frac12$$ $$P(BT_1\leq r)=\frac12$$ Since, the events $(1)$ and $(2)$ are independent, we have $$P(AT_1+BT_2=AB\leq 2r)=\frac12.$$