Find the center of all circles that touch the $x$-axis and a circle centered at the origin

Question

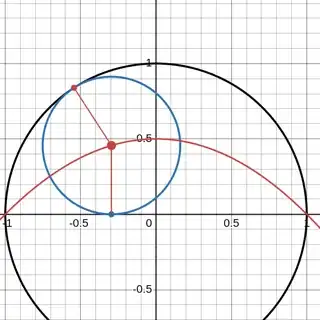
Given a circle $C$ of radius $1$ centered at the origin, I want to determine the locus of the centers of all circles that touch $C$ and the $x$-axis. This is the red curve in the following Desmos plot, where the blue circle touches $C$ and the $x$-axis:

Let $P=(\sin\alpha,\cos\alpha)$ be the point where the blue circle touches $C$. Moving $\ell$ units towards the center of $C$ (the origin) gives the point $Q=(1-\ell)(\sin\alpha,\cos\alpha)$. Now a circle around $Q$ touches the $x$-axis when the $y$-coordinate of $Q$ equals $\ell$, so that $Q$ has the same distance to $C$ and to $y=0$:

$$ Q_y=(1-\ell)\cos\alpha \stackrel.= \ell \tag1 $$

This equation is solved by $$Q_y=\frac{\cos\alpha}{1+\cos\alpha} \tag2$$ It's also easy to compute the $x$-ccordinate of $Q$, which yields $Q$ depending on $\alpha$: $$ Q=Q(\alpha)=\left(\frac{\sin\alpha}{1+\cos\alpha}, \frac{\cos\alpha}{1+\cos\alpha}\right) \tag3 $$

Where I am stuck is to compute $Q_y$ as a function of $Q_x$, that is find $f$ such that

$$ Q_y = f(Q_x) \tag4 $$

By looking at the plot I guessed $$ f(t) = \frac12(1-t^2) \tag 5 $$ and indeed $Q$ satisfies $(5)$. It's not surprising that $f$ is a curve or order 2. But how to do it without guessing? I have no idea how to find the inverse of

$$ \alpha \mapsto \frac{\sin\alpha}{1+\cos\alpha} $$ Trying to substitute $\alpha = \arcsin z$ gives $$ Q(z) = \left(\frac z{1+\sqrt{1-z^2}} , \frac{\sqrt{1-z^2}}{1+\sqrt{1-z^2}} \right)\tag6 $$ just makes it more complicated...

Answer 1

The radius of a blue circle is $y$. The distance between the centers is $1-y$ (do you see why?). Therefore, $x^2 + y^2 = (1-y)^2$.

Answer 2

Let the centre of the circle be $C = (h,r).$
since this circle touches $x^2 + y^2 = 1$ internally,
$|OC| = 1 - r.$
$\implies h^2+r^2 = (1-r)^2.$
$\implies h^2 = 1 - 2r.$
$\implies h = \sqrt{1-2r}$
or $ r = \displaystyle\frac{1-h^2}{2}.$

Answer 3

I have no idea how to find the inverse of $$\alpha \mapsto \frac{\sin\alpha}{1+\cos\alpha}$$

When manipulating trig expressions, always be on the lookout to utilise the fundamental Pythagorean identity,
$$\sin^2\alpha + \cos^2\alpha=1$$

Note that $$\sin^2\alpha = 1-\cos^2\alpha = (1+\cos\alpha)(1-\cos\alpha)$$ So $$\frac{\sin\alpha}{1+\cos\alpha} = \frac{1-\cos\alpha}{\sin\alpha}$$

Let $$u = \frac{\sin\alpha}{1+\cos\alpha} = \frac{1-\cos\alpha}{\sin\alpha}$$ Thus $$u^2 = \left(\frac{\sin\alpha}{1+\cos\alpha}\right) \left(\frac{1-\cos\alpha}{\sin\alpha}\right)$$ That is, $$u^2 = \frac{1-\cos\alpha}{1+\cos\alpha}$$ which is easy to invert: $$\cos\alpha = \frac{1-u^2}{1+u^2}$$

Also, $$\sin\alpha = \frac{2u}{1+u^2}$$ So $$\tan\alpha = \frac{2u}{1-u^2}$$ Hence $$u=\tan\frac{\alpha}{2}$$

Answer 4

With the arcsin substitution you had ended up with:

$$Q(z) = \left(\frac z{1+\sqrt{1-z^2}} , \frac{\sqrt{1-z^2}}{1+\sqrt{1-z^2}} \right)\tag6$$

It looks harder than it really is. You just have to press on:

$$\begin{aligned} x &= \frac z{1+\sqrt{1-z^2}} \\ \frac z x - 1 &= \sqrt{1-z^2} \\ \frac{z^2}{x^2} - \frac{2 z}{x} + 1 &= 1 - z^2 \\ \left(\frac{1}{x^2} + 1\right)z^2 - \frac{2 z}{x} &= 0 \\ \left(1 + x^2\right)z - 2 x &= 0 \\ z &= \frac{2 x}{1 + x^2} \end{aligned}$$

(Note that $z = 0$ is a spurious solution coming from $z/x - 1 = {\color{red}-}\sqrt{1-z^2}$, which we can disregard.)

Then we evaluate $y$:

$$\begin{aligned} z &= \frac{2 x}{1 + x^2} \\ z^2 &= \frac{4 x^2}{(1 + x^2)^2} \\ 1 - z^2 &= \frac{1 + 2 x^2 + x^4 - 4 x^2}{(1 + x^2)^2} \\ &= \frac{1 - 2 x^2 + x^4}{(1 + x^2)^2} \\ &= \frac{(1 - x^2)^2}{(1 + x^2)^2} \\ \sqrt{1 - z^2} &= \frac{1 - x^2}{1 + x^2} \\ y &= \frac{\sqrt{1-z^2}}{1 + \sqrt{1-z^2}} \\ &= \frac{(1 + x^2) \sqrt{1-z^2}}{1 + x^2 + (1 + x^2) \sqrt{1-z^2}} \\ &= \frac{1 - x^2}{1 + x^2 + 1 - x^2} \\ &= \frac{1 - x^2}{2} \end{aligned}$$

Answer 5

Draw a line tangent to the circle at the top and parallel to the $x$-axis. Show that:

• At points inside the circle, the distances to the tangent line and the center of the circle are both $R-d$, where $d$ is the distance to the circle itself (or to the $x$-) and $R$ is the radius of the circle.

• At points outside the circle, the distances to the tangent line and tge center are both $R+d$.

The conic section equidistant from a point and a line is a parabola.