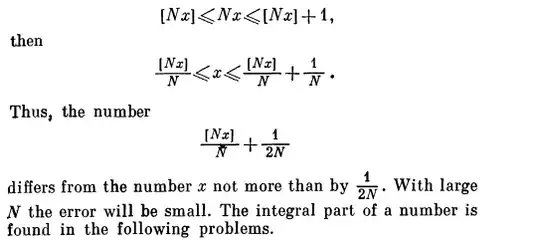Here, $[ \cdot]$ is $\lfloor \cdot \rfloor $ floor function.
N $ \in N$. Where did $\frac{[Nx]} N + \frac{1}{2N}$ came from
and how does $x$ differs by $\frac{1}{2N}$. Shouldn't it be
$\frac{1}N$ if $x$ is an integer.
- 30,485
-
fixed @Moo .thanks !! – Yugant Shewale Feb 20 '24 at 14:09
2 Answers
Let $a=\frac{[Nx]}{N}$ and $b= \frac{[Nx]}{N} +\frac{1}{N}$
$\frac{[Nx]}{N} +\frac{1}{2N}=\frac{a+b}{2}$ is the midpoint of $a$ and $b$. By the first sets inequalities, we know that $x$ is between these $a$ and $b$. Thus:
$$a\leq x \leq b$$ $$\implies$$ $$a\leq x \leq \frac{a+b}{2} \mbox{ or } \frac{a+b}{2}\leq x \leq b$$ (This describes the three cases: $x$ is to the right of the midpoint, to the left of the midpoint, or on the midpoint).
In all of these cases, $x$ is not further away from either $a$ or $b$ than their midpoint. And clearly, the midpoint is distance $\frac{1}{2N}$ from either. Thus we get the bound described.
- 1,928
The double inequality $$\frac{\lfloor Nx\rfloor}N \leqslant x \leqslant \frac{\lfloor Nx\rfloor}N + \frac 1N$$ describes an interval containing the $x$ value: $$x\in\left [ \frac{\lfloor Nx\rfloor}N , \frac{\lfloor Nx\rfloor}N + \frac 1N \right]$$
The interval starts at $\frac{\lfloor Nx\rfloor}N$ and its length is $\frac 1N$, so the value $$\frac{\lfloor Nx\rfloor}N + \frac 1{2N}$$ is just a midpoint of the interval.
And any $x$ in the interval differs from the interval's midpoint by not more than a half of the interval's length: $$\left|x - \left(\frac{\lfloor Nx\rfloor}N + \frac 1{2N}\right)\right| \leqslant \frac 1{2N}$$
- 13,884
-
Thanks!!! Even though my question was so dumb you answered thanks for that – Yugant Shewale Feb 20 '24 at 14:14
-
1@YugantShewale Your question is not 'dumb' :D Everyone was once a beginner, and everyone can misread or misunderstand something. As long as you really try to get through and make a decent effort to explain your problem to get an answer, the question is valid and it deserves explanation and answer. – CiaPan Feb 21 '24 at 06:51
-
1Comment to myself re 'Everyone was once a beginner' – if you look from an experience level high enough, everyone is still a beginner.... – CiaPan Feb 21 '24 at 07:31