Ring Structure on the geometric line in synthetic geometry

Question

Synthetic Differential Geometry by Kock opens with the following:

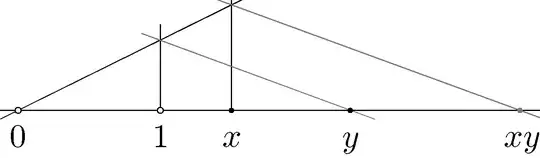
The geometric line can, as soon as one chooses two distinct points on it, be made into a commutative ring, with the two points as respectively 0 and 1. This is a decisive structure on it, already known and considered by Euclid, who assumes that his reader is able to move line segments around in the plane (which gives addition), and who teaches his reader how he, with ruler and compass, can construct the fourth proportional of three line segments; taking one of these to be [0, 1], this defines the product of the two others, and thus the multiplication on the line...Of course, this basic structure does not depend on having the (arithmetically constructed) real numbers $\mathbb{R}$ as a mathematical model for [it]).

I am confused about what exactly this ring structure is? Am I to understand that the elements of this Ring are not points on the line but line segements? Does one add two line segements by just adding their length? I looked up how to construct the fourth proportional of three line segments which is multiplication in this ring, leading me to suspect that perhaps he's referring to the ring of geometrically constructible numbers?

Answer 1

The ring structure on the geometric line $R$ with two distinguished points labeled $0$ and $1$ respectively arises as follows:

• The points of the line constitute the elements of the ring (not line segments as you assumed).

• The sum of two points $x,y$ is obtained by translating the line segment between $0$ and $x$ so that the endpoint that originally sat at $0$ before translation now sits at $y$. The other endpoint of this line segment is defined as the sum, the point $x+y$.

• The product of two points $x,y$ arises via the "fourth proportional" construction on three line segments: the line $R$ is the horizontal line on the bottom of the diagram below, and the product is the point labeled $xy$. The first two line segments are the ones determined by $0$ and the inputs $x,y$. The third line segment is the one that goes from $0$ to $1$.

• One can prove that, as long as this "geometric line object" $R$ that we start with satisfies some reasonable geometric axioms (e.g. you could take Tarski's axioms for plane geometry), the sum and product operations defined in this manner will satisfy the commutative ring axioms. The additive identity is the distinguished point $0$ of the line $R$, the multiplicative identity is the point $1$.

The ring defined this way depends strongly on the geometric line object you start with. E.g the usual affine space $\mathbb{R}^2$ familiar from set theory is a model of a geometric plane, and the ring you get this way is then isomorphic to $\mathbb{R}$, so contains many more numbers than the so-called "geometrically constructible numbers" you read about (but to be honest that particular set is largely a red herring here).

Kock's point is that one need not start with the arithmetically constructed set of real numbers (i.e. the set-theoretic $\mathbb{R}$ you construct in undergraduate Real analysis: starting with the integers, creating a fraction field to obtain the rationals, then Dedekind cuts to obtain the reals). This basic way of constructing a ring on a line inside a geometric plane does not depend on specifically having the (product of two copies of the classical arithmetically constructed) real numbers as that plane. Indeed, he'll shortly axiomatize and study a ring that cannot arise from the usual arithmetically constructed reals this way, but is nonetheless geometric.