κ₀ for Mercury—Formula

Question

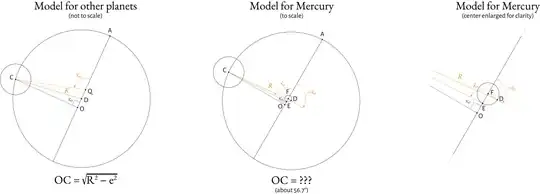
I refer here to Ptolemy’s epicycle-and-deferent model of the Solar System, specifically that of Mercury (see drawing).

In this model, Mercury (not shown) revolves on an epicycle of center C, which itself turns on an eccentric circle (later called “deferent”) of center D, which in turn moves on a small circle of center F. The size of this small circle is such that DF = FE = EO = 3 arbitrary units where DC = 60 of the same units.

Point A is the direction of the apogee, the deferent’s point which is furthest from the Earth. Angle AFD increases uniformly and is called the mean centrum $ \bar{\kappa} $. The true centrum, $ \kappa $, is angle AOC—obviously, this one does not increase uniformly, and a good part of the Almagest consists of the explanation of the procedure to find it.

The calculation of latitudes involves finding out distance OC for when $ \kappa = 90° $. Its calculation is not mentioned in Ptolemy’s Almagest, but its value in the model for Mercury is specified as being about 56.7° (Ptolemy actually says it was found previously, but such is not the case). For other planets, for which the deferent is fixed and centered where point E is for Mercury, the calculation is easy: $ \displaystyle OC = \sqrt{R^2 - e^2} $, but the calculation is made more complex in Mercury’s case, because the deferent moves, with angle AFD equal to (but in opposite direction from) angle AEC, in both cases being $ \bar{\kappa} $.

In A History of Ancient Mathematical Astronomy, Otto Neugebauer states that, in order to find this value, “One finds a cubic equation for the sine of the angle under which the eccentricity e = 3 is seen from C” (p. 221, n. 1).

I have looked in other books and articles commenting the Almagest, but I have never been able to find the said “cubic equation for the sine of the angle.”

Can someone please help me find this equation?

Answer 1

Too long to comment :

I don't know how to get a cubic equation for the sine of $\bar{\kappa_0}$, but I got a cubic equation for the cosine of $\bar{\kappa_0}$, which might interest you.

In the following, I'm going to show how to get the equation. One can get the equation using the law of sines and the law of cosines.

Let $x:=\bar{\kappa_0}$ and $c:=\cos x$.

Let $G$ be the intersection point of $EF$ with $CD$.

Let $H$ be a point on $EF$ such that $DH\perp EF$.

Considering a right triangle $CEO$ with $\angle{CEO}=180-x$, we have $$CE=\frac{3}{\cos(180-x)}=\frac{-3}{c}\tag1$$

Applying the law of sines to $\triangle{DFG}$, we have $$\sin\angle{DGF}=\frac{3\sin(180-x)}{DG}\tag2$$

Applying the law of sines to $\triangle{CEG}$, we have $$\sin\angle{CGE}=\frac{CE\sin x}{60-DG}\tag3$$

From $(2)(3)$, we get $$\frac{3\sin(180-x)}{DG}=\frac{CE\sin x}{60-DG}$$ so using $(1)$, $$DG=\frac{60c}{c-1}\tag4$$

Applying the law of cosines to $\triangle{FDG}$, we have $$DG^2=9+FG^2-2\cdot 3\cdot FG\cos(180-x)$$ which can be written as $$DG^2-FG^2=9+6FGc\tag5$$

Applying the law of cosines to $\triangle{CEG}$, we have $$(60-DG)^2=(3-FG)^2+CE^2-2\cdot CE(3-FG)c$$ which can be written as $$DG^2-FG^2=-3573+120DG-12FG+\frac{9}{c^2}\tag6$$

From $(5)(6)$, we get $$9+6FGc=-3573+120DG-12FG+\frac{9}{c^2}$$ so using $(4)$, $$FG=\frac{3 (402 c^3 + 398 c^2 + c - 1)}{2c^2(c - 1)(c+2)}\tag7$$

Since $\triangle{GHD}\sim\triangle{GOC}$, we have $$DH:CO=GH:GO\tag8$$ Since $DH=3\sin x,CO=-3\tan x$ and $GO=6+3c-GH$, it follows from $(8)$ that $$GH=\frac{(6+3c)\sin x}{\sin x-\tan x}=\frac{3c(c+2)}{c-1}$$

So, we get $$FG=FH+GH=-3c+\frac{3c(c+2)}{c-1}\tag9$$

It follows from $(7)(9)$ that $$\frac{3 (402 c^3 + 398 c^2 + c - 1)}{2c^2(c - 1)(c+2)}=-3c+\frac{3c(c+2)}{c-1}$$ i.e. $$\frac{(c + 1) (6 c^3 - 396 c^2 - 2 c + 1)}{c(c-1)(c+2)}=0$$

Since $c\not=-1$, we get
$$\color{red}{6 \cos^3\bar{\kappa_0} - 396\cos^2\bar{\kappa_0} - 2\cos\bar{\kappa_0} + 1=0}$$

It follows from $(1)$ that $\cos\bar{\kappa_0}$ has to be negative.

According to WolframAlpha, the only negative solution is $$\cos \bar{\kappa_0}\approx -0.052818361$$ which gives $$OC=3\sqrt{\frac{1}{\cos^2\bar{\kappa_0}}-1}\approx 56.7191$$