Background
In a previous question, user Trevor asked whether the ratio of "chaotic" to preceding "non chaotic" cells in a particular cellular automaton tended to the golden ratio. Here is their original picture: the automaton in question is a variation of Rule 30 on an alternating cell background.
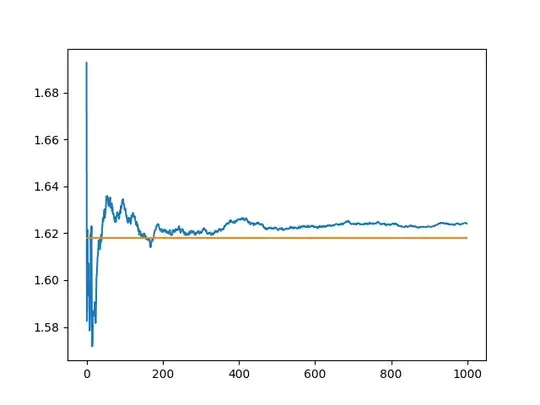
Indeed, his claim seemed realistic at first, but then, in my answer, I noted that by crunching the numbers some more, the ratio seemed to approach another value, likely larger than $1.62$.
The $999000$th computed value was $1.62414531$ (i do not have the 1 million-th one, I did not print it because of an off-by-one bug in my code). The average of the last 30 reported results, each a thousand iterations apart, is: 1.6240807783333333
The original author was satisfied, and accepted the answer. Despite this, I am not at all satisfied.
My question
Would it be possible to explain why (or, whether) the ratio approaches a constant at all? And could it be possible to find the exact ratio?
A simple proof by induction is able to describe the behavior of the messy part on its right boundary. However, the behavior on the left seems chaotic, and is likely non-repeating. Maybe using some probabilistic approach could describe it, and provide an intuition for this apparent convergence?
References
The original automaton is described here.