How to solve this integral using contour integration:$$\int_{-\infty}^{\infty} \frac{\cos px - \cos qx}{x^2} dx \stackrel{?}{=} \pi (q-p)$$
Here is what I have tried: I don't know if I can use Residue theorem, as it has a pole of second order on the real axis, which is not simple. So I am stuck.
Residue theorem can be avoided altogether. Notice that
$$\int_{-\infty}^\infty \frac{\cos px-\cos qx}{x^2}dx = \operatorname{Re}\left\{\int_{-\infty}^\infty \frac{e^{ipx}-e^{iqx}-i(q-p)x}{x^2}dx\right\}$$
which we will denote $\int_\Bbb{R}f(z)dz$. This function has no poles and is holomorphic everywhere, therefore any closed loop line integral of this function is $0$. This gives us
$$0=\int_{[-R,R]}f(z)dz + \int_{|z|=R}f(z)dz$$
where the second integral is taken over the semicircle in the upper half plane. Since this equality is true for all values of $R$, simply take the limit as $R\to\infty $:
$$\int_\Bbb{R}f(z)dz = \lim_{R\to\infty}-\int_0^\pi\frac{e^{ipRe^{i\theta}}-e^{iqRe^{i\theta}}-i(p-q)Re^{i\theta}}{R^2e^{i2\theta}}\cdot\left(iRe^{i\theta}d\theta\right)$$
$$\longrightarrow (q-p)\int_0^\pi d\theta = \boxed{\pi(q-p)}$$
The answer is already real so there are no more simplifications to be made.
I will assume that $p, q \geq 0$, for otherwise the equality is false.
Method 1. Let me demonstrate a method that only relies on contour integration. Consider the contour $\mathcal{C} = \mathcal{C}_{R,\epsilon}$ of the form
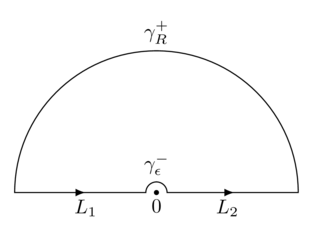
where $\gamma_R^+$ (resp. $\gamma^-_{\epsilon}$) is the CCW-oriented (resp. CW-oriented) upper semicircular arc of radius $R$ (resp. $\epsilon$). Then by the residue theorem,
\begin{align*} 0 &= \oint_{\mathcal{C}} \frac{e^{ipz} - e^{iqz}}{z^2} \, \mathrm{d}z \\ &= \int_{L_1 \cup L_2} \frac{e^{ipx} - e^{iqx}}{x^2} \, \mathrm{d}x + \int_{\gamma^+_{R}} \frac{e^{ipz} - e^{iqz}}{z^2} \, \mathrm{d}z + \int_{\gamma^-_{\epsilon}} \frac{e^{ipz} - e^{iqz}}{z^2} \, \mathrm{d}z. \end{align*}
The first integral becomes
$$ \int_{L_1 \cup L_2} \frac{e^{ipx} - e^{iqx}}{x^2} \, \mathrm{d}x = \int_{L_1 \cup L_2} \frac{\cos(px) - \cos(qx)}{x^2} \, \mathrm{d}x, $$
which converges to the OP's integral as $R \to \infty$ and $\epsilon \to 0^+$. For the second integral, note that
$$ \left| \int_{\gamma^+_{R}} \frac{e^{ipz} - e^{iqz}}{z^2} \, \mathrm{d}z \right| \leq \int_{\gamma^+_{R}} \frac{|e^{ipz} - e^{iqz}|}{|z|^2} \, |\mathrm{d}z| \leq \int_{\gamma^+_{R}} \frac{2}{R^2} \, |\mathrm{d}z| = \frac{2\pi}{R} \to 0 $$
as $R \to \infty$. Hence the integral vanishes in the limit. Finally, noting that $e^z = 1 + z + \mathcal{O}(z^2)$ as $z \to 0$,
\begin{align*} \int_{\gamma^-_{\epsilon}} \frac{e^{ipz} - e^{iqz}}{z^2} \, \mathrm{d}z &= \int_{\gamma^-_{\epsilon}} \biggl( \frac{i(p-q)}{z} + \mathcal{O}(1) \biggr) \, \mathrm{d}z \\ &= -\int_{0}^{\pi} \biggl( \frac{i(p-q)}{\epsilon e^{i\theta}} + \mathcal{O}(1) \biggr) \, (i\epsilon e^{i\theta}) \mathrm{d}\theta \\ &= (p-q)\pi + \mathcal{O}(\epsilon). \end{align*}
Hence this integral converges to $(p-q)\pi$ as $\epsilon \to 0^+$. Finally, combining all these computations together, we get
$$ 0 = \lim_{\substack{R \to \infty \\ \epsilon \to 0^+}} \oint_{\mathcal{C}} \frac{e^{ipz} - e^{iqz}}{z^2} \, \mathrm{d}z = \int_{-\infty}^{\infty} \frac{\cos(px) - \cos(qx)}{x^2} \, \mathrm{d}x + (p-q)\pi, $$
proving the desired equality.
Method 2. Assuming OP is aware of the formula
$$ \int_{-\infty}^{\infty} \frac{\sin(ax)}{x} \, \mathrm{d}x = \pi \operatorname{sgn}(a), $$
which can also be proved by contour integration technique or else, we can come up with a very short proof: By integration by parts,
\begin{align*} \require{cancel} &\int_{-\infty}^{\infty} \frac{\cos(px) - \cos(qx)}{x^2} \, \mathrm{d}x \\ &= \cancel{\left[ -\frac{\cos(px) - \cos(qx)}{x} \right]_{-\infty}^{\infty}} - \int_{-\infty}^{\infty} \frac{p \sin(px) - q \sin (qx)}{x} \, \mathrm{d}x \\ &= -(p \pi \operatorname{sgn}(p) - q \pi \operatorname{sgn}(q)) \\ &= (|q| - |p|)\pi. \end{align*}
